출처
접근
완전탐색(DFS)
각 연산자의 우선순위를 변경하면서 전체 탐색을 하고, 변경된 우선순위마다 수식을 계산해서 최댓값을 갱신합니다.
- 연산자 순서에 따라 결과가 달라지므로, 순열(Permutation)에 해당합니다.
다양한 구현방법이 있지만, 개인적으로 다양한 조건을 만족하는 순열(조합)을 빠르게 구현할 수 있는
DFS를 선호합니다.
- 3가지 연산자만 있으므로, 모든 경우의 수를 구해도
6가지이기 때문에 시간복잡도는 충분합니다.
후위 표기 변환(InFix to PostFix)
보통 사람이 계산을 할 때는
A + B * C의 형태로 수식을 써서 계산을 합니다. 이 때, A와 B 사이에 연산자가 있는 형태를 중위 표기(InFix)라고 합니다.그러나, 컴퓨터는 이러한 계산을
A B C * +의 형태로 변환해서 숫자 이후에 연산자가 나오는 형태로 변경한 뒤, 스택에 옮겨 계산하게 됩니다. 이러한 표기법을 후위 표기(PostFix)라고 합니다.후위 표기법은 연산의 우선순위에 따라 쉽게 수식을 표현하고, 계산할 수 있다는 장점이 있습니다.
이번 풀이에서도 이러한 후위 표기법을 구현하여 문제를 해결하겠습니다.
중위 표기 -> 후위 표기의 변환과정 (Infix -> Postfix)을 자세히 살펴보면 다음과 같습니다.
- 결과를 담을 큐와 연산자를 임시 저장할 스택을 정의합니다.
- 중위 표기에서 숫자가 나오면 바로 큐에 삽입합니다.
- 중위 표기에서 연산자가 나오면 다음 절차를 수행합니다.
- 현재 저장된 스택에 현재 연산자보다 우선순위가 큰 연산자가 나올때까지 스택을 비웁니다.
- 현재 연산자를 스택에 저장합니다.
- 모든 중위 표기 원소를 확인한 후, 스택이 비어있지 않다면 해당 연산자들을 순차적으로 큐에 삽입합니다.
위 과정을 그림과 함께 순서대로 보겠습니다.
아래는 문제에서 주어진 1번 예제에서 정답인
(우선순위 : X -> + -> -)의 답을 구하는 과정입니다.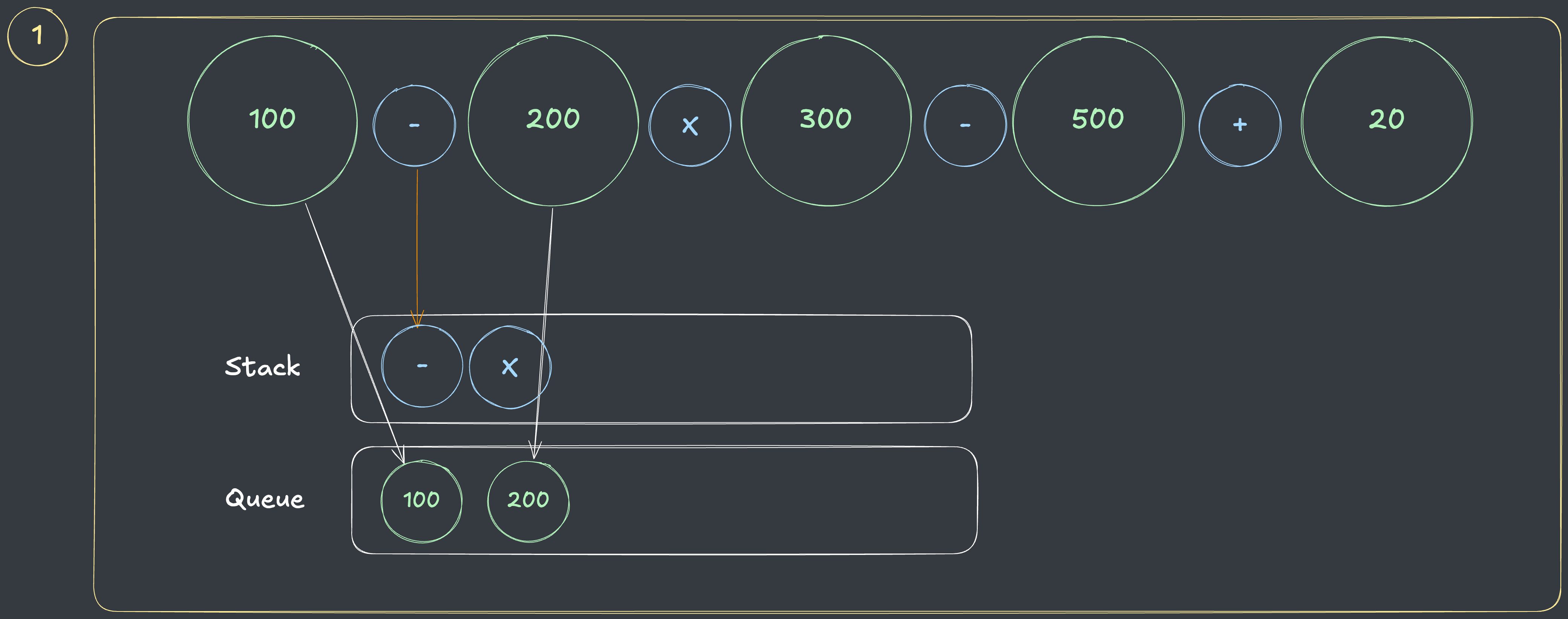
- 숫자
(100, 200)들은 큐에 바로 담고, 첫번째 연산자인-는 스택이 비었으므로 바로 담습니다.
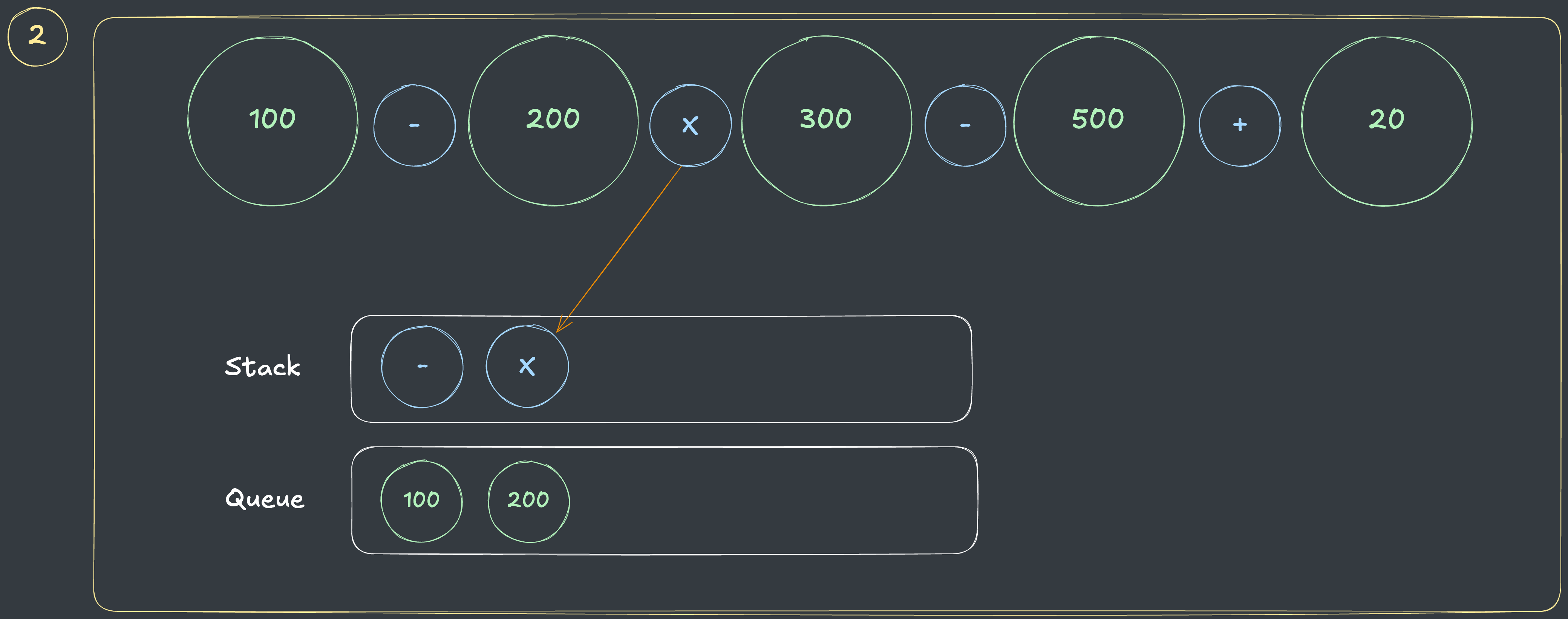
- 두번째 연산자인
X는 스택에 담고, 해당 연산자보다 우선순위가 큰 연산자는 없으므로, 스택에서 연산자를 제거하지 않습니다.
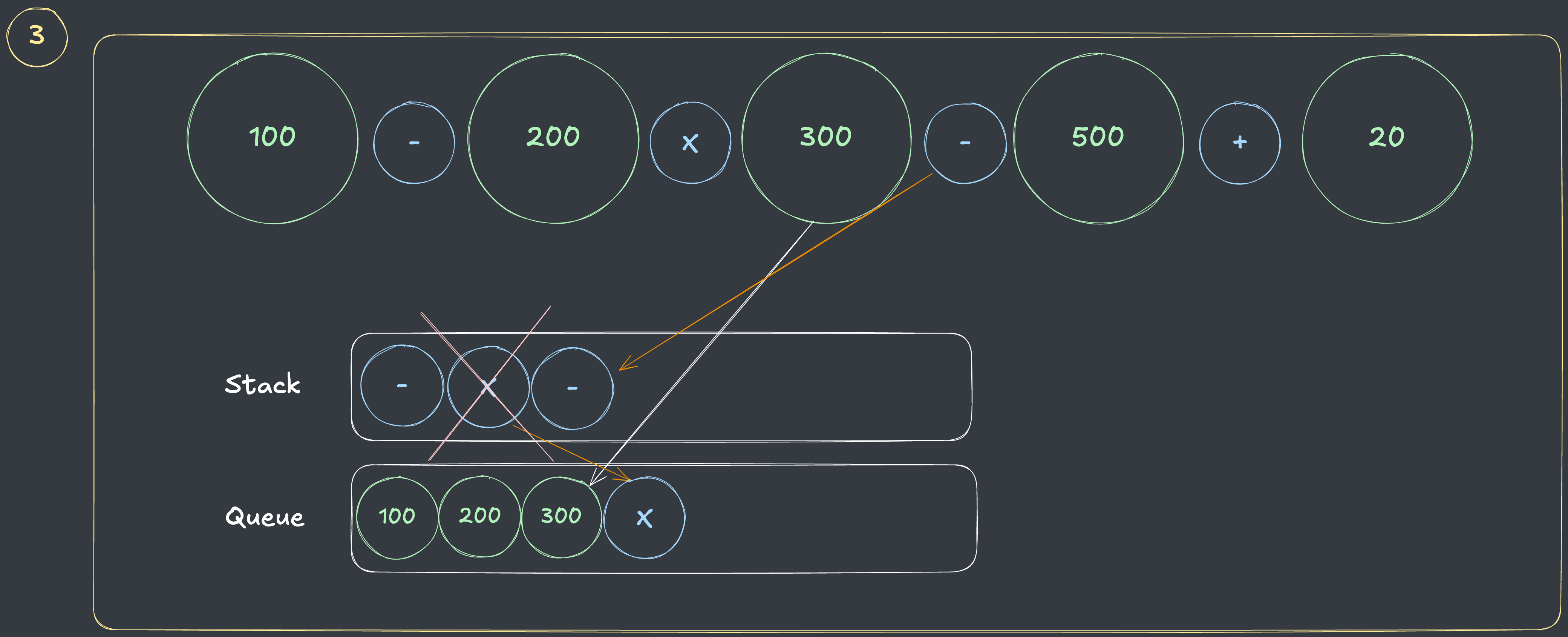
- 숫자
300은 바로 큐에 담고, 세번째 연산자인-를 스택에 담는 과정에서 해당 연산자보다 우선순위가 큰 연산자인X를 큐에 담습니다.
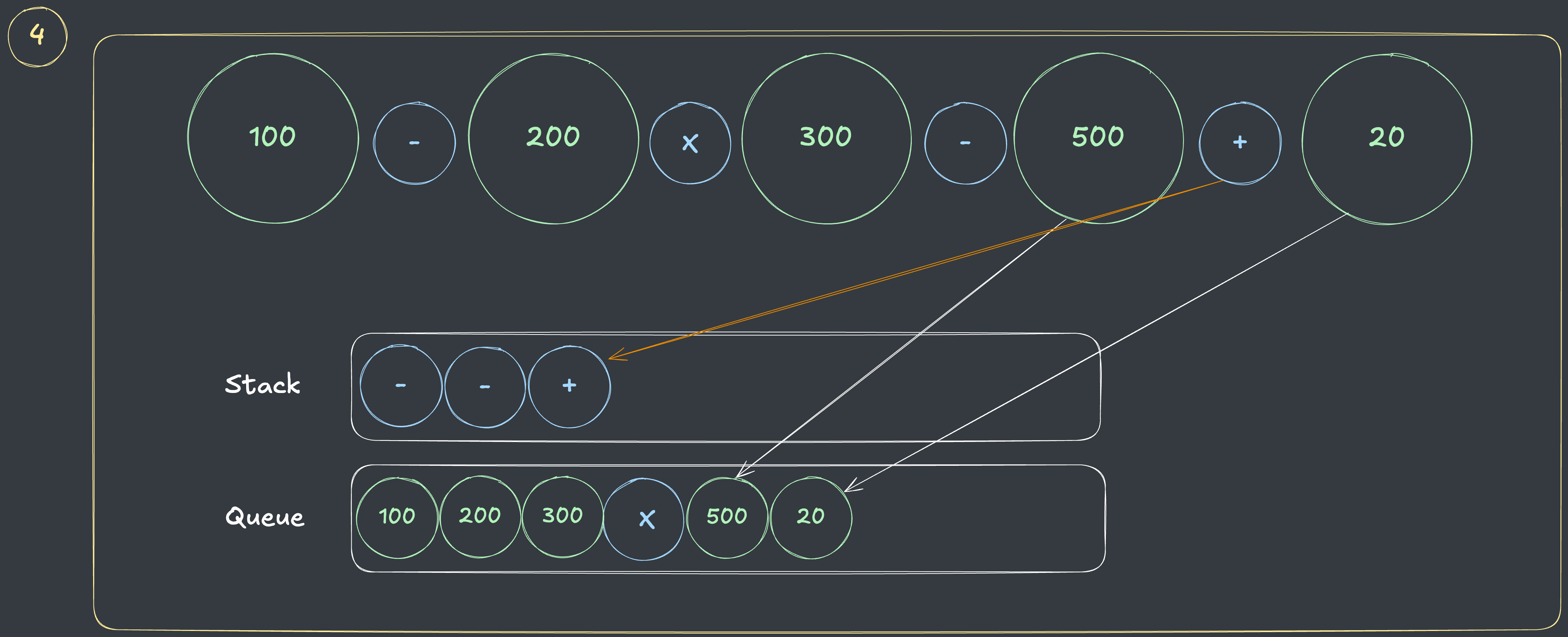
- 나머지 숫자
(500, 20)를 큐에 담고, 네번째 연산자인+를 담는 과정에서 스택의 첫번째 연산자(-)가 해당 연산자보다 우선운위가 작으므로 스텍에서 연산자를 제거하지 않습니다.
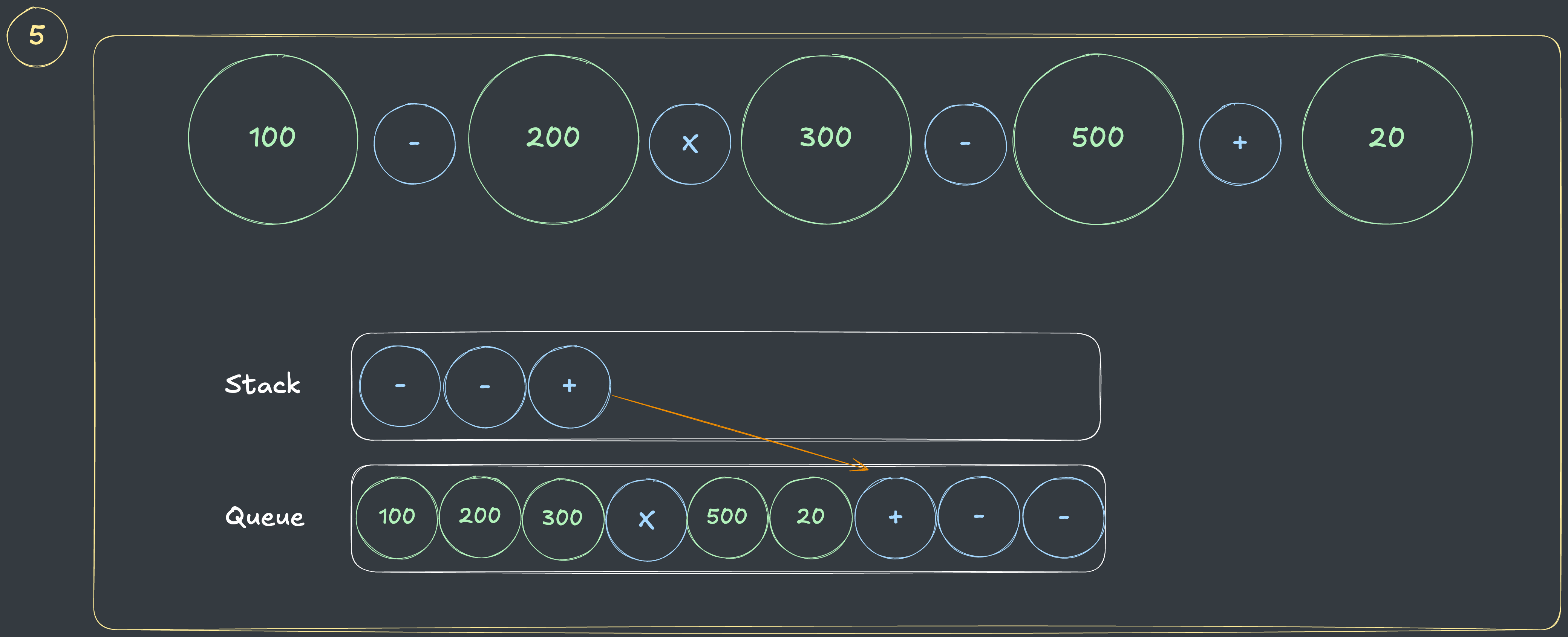
- 중위 표기의 모든 원소를 확인했는데, 스택이 아직 비어있지 않으므로 스택의 모든 연산자를 큐에 추가합니다.
- 숫자
후위 표기 계산
후위 표기를 계산할 때는 숫자들을 임시 저장할 스택을 생성하고, 완료된 숫자들을 저장하면서 계산합니다.
후위 표기법의 계산 과정을 자세히 살펴보면 다음과 같습니다.
- 숫자를 임시 저장할 스택을 정의합니다.
- 숫자가 나오면 스택에 담습니다.
- 연산자가 나오면 스택에서 숫자를 꺼내 계산한 뒤, 다시 스택에 넣습니다.
위 과정을 그림과 함께 순서대로 보겠습니다.
위에서 변환한 큐를 계산하는 과정입니다.
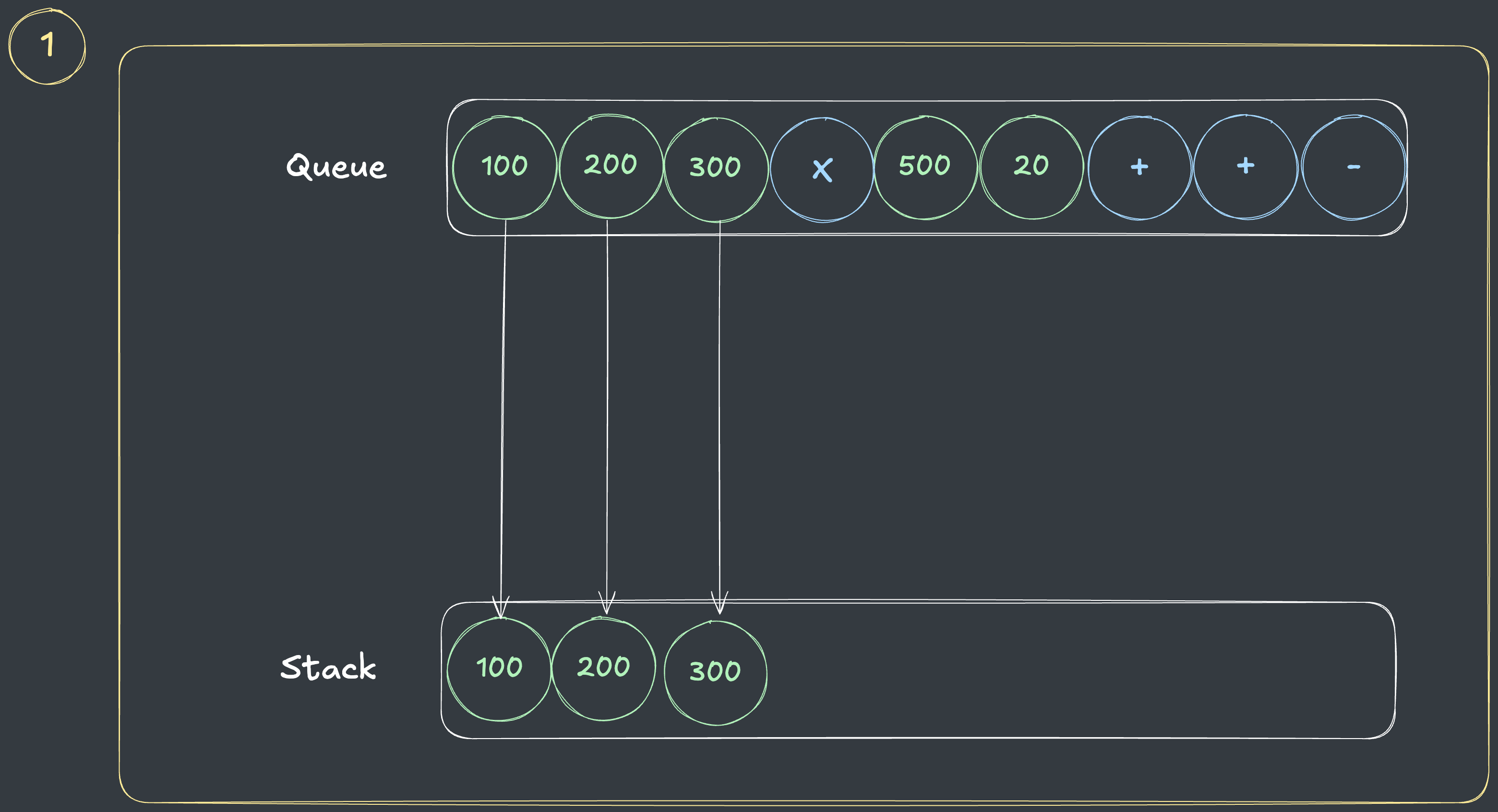
- 연산자가 나올때까지 모든 숫자를 스택에 담습니다.
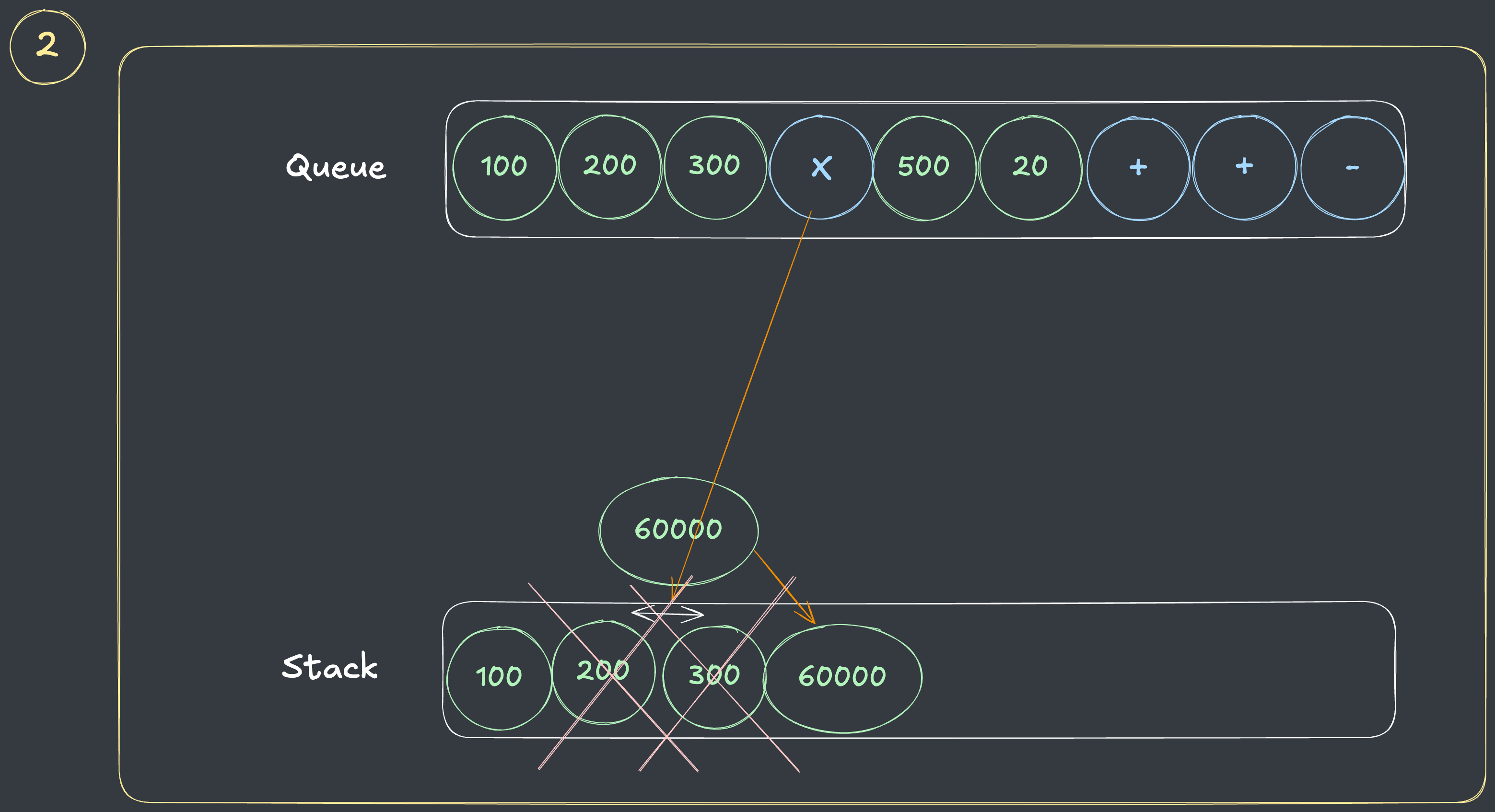
- 연산자가 나오면 스택에서 2개를 꺼내 계산합니다.
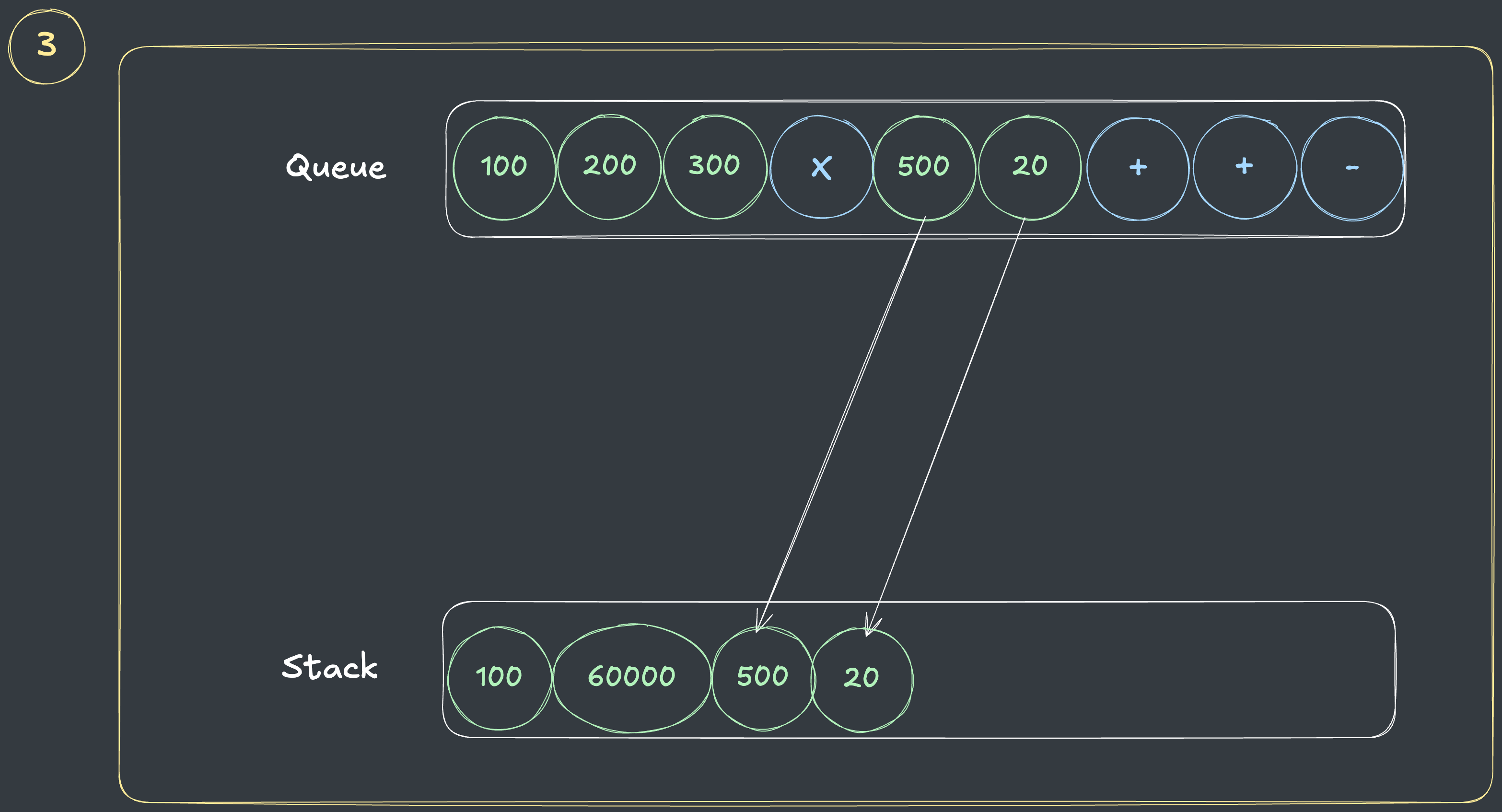
- 다시 연산자가 나올때까지 모든 숫자를 스택에 담습니다.
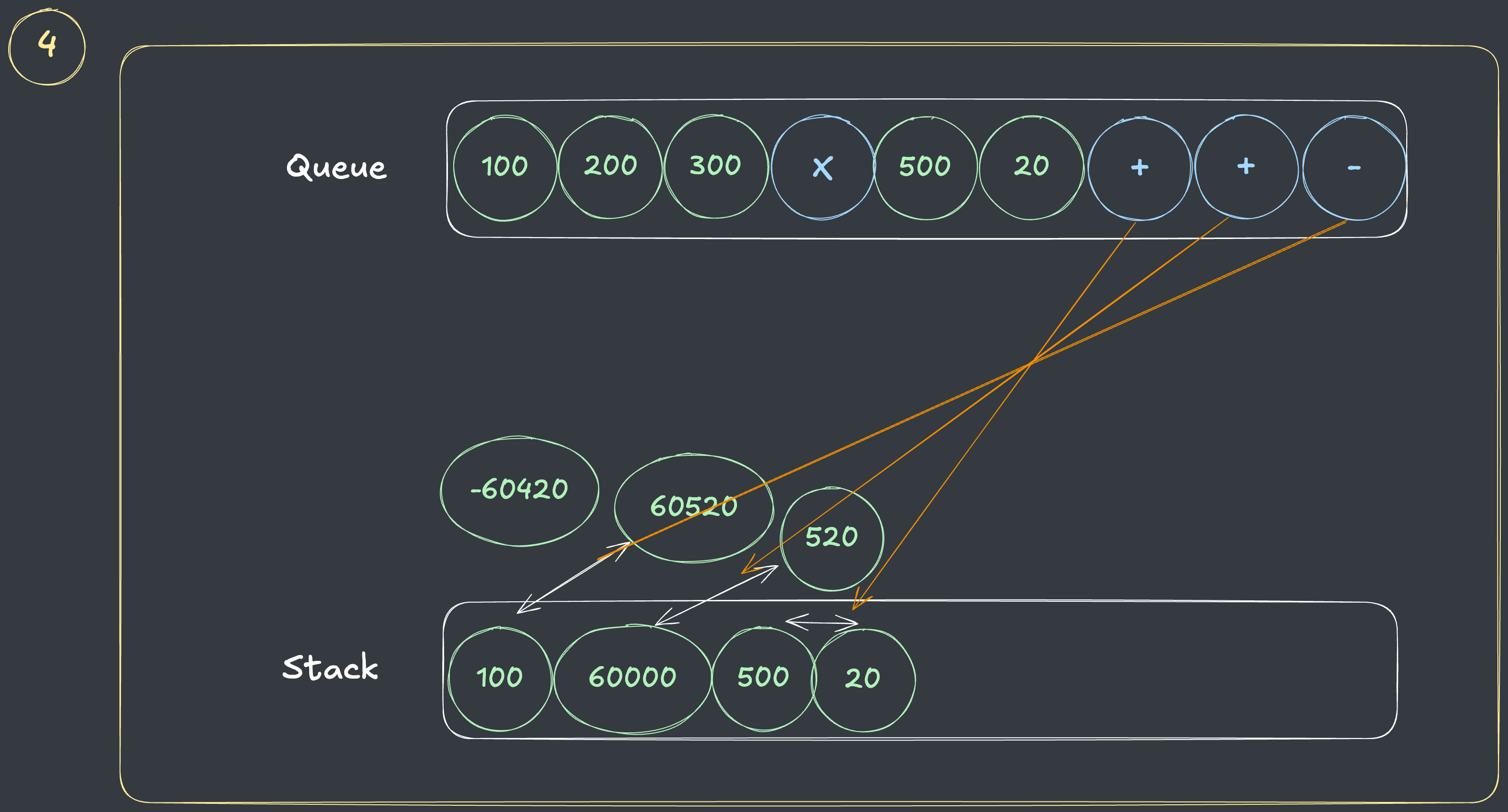
- 연산자마다 스택에서 2개씩 숫자를 꺼내 계산합니다.
문제에서는 계산 결과의 절댓값을 구해야 하므로, 정답인
60420을 얻을 수 있습니다.
풀이
import java.util.*;
class Solution {
long answer = 0;
List<String> exps = new ArrayList<>();
public long solution(String expression) {
parse(expression);
dfs(new char[3], 0, new boolean[4]);
return answer;
}
// 주어진 문자열에서 숫자와 연산자 분리
void parse(String e) {
StringBuilder sb = new StringBuilder();
for (char c : e.toCharArray()) {
if (c - '0' < 0) {
exps.add(sb.toString());
exps.add(new String(new char[]{c}));
sb = new StringBuilder();
} else {
sb.append(c);
}
}
exps.add(sb.toString());
}
// 연산자 순열 구하기(3! = 6)
char[] exp = {'+', '-', '*'};
void dfs(char[] priority, int now, boolean[] isAdded) {
if (now == 3) {
answer = Math.max(answer, calculate(priority));
return;
}
for (char c : exp) {
if (isAdded[c - '*']) continue;
isAdded[c - '*'] = true;
priority[now] = c;
dfs(priority, now + 1, isAdded);
isAdded[c - '*'] = false;
}
}
// 숫자 계산
long calculate(char[] priority) {
Deque<String> q = infixToPostfix(priority);
// 숫자들을 임시 저장할 스택
Stack<Long> temp2 = new Stack<>();
while (!q.isEmpty()) {
String e = q.poll();
// 연산자일 경우 스택에서 2개를 꺼내서 계산 후 결과값 스택으로 이동
if (e.equals("*") || e.equals("+") || e.equals("-")) {
long i2 = temp2.pop();
long i1 = temp2.pop();
temp2.push(calc(e, i1, i2));
} else {
// 숫자는 바로 스택으로 이동
temp2.push(Long.parseLong(e));
}
}
return Math.abs(temp2.pop());
}
// 중위 표기 -> 후위표기 변환
Deque<String> infixToPostfix(char[] priority) {
Deque<String> q = new ArrayDeque<>();
Stack<String> temp = new Stack<>();
for (String e : exps) {
if (e.equals("*") || e.equals("+") || e.equals("-")) {
// 현재 숫자보다 우선순위가 크거나 같은 연산자들을 모두 스택에서 큐로 이동
while (!temp.isEmpty() && getPriority(priority, temp.peek()) >= getPriority(priority, e)) {
q.offer(temp.pop());
}
// 현재 연산자 스택에 보관
temp.push(e);
} else {
// 숫자는 바로 큐에 넣기
q.offer(e);
}
}
// 연산자가 스택에 남아있다면 큐로 이동
while (!temp.isEmpty()) q.offer(temp.pop());
return q;
}
// 문자열인 계산식과 숫자들을 받아서 계산
long calc(String c, long i1, long i2) {
switch (c.charAt(0)) {
case '+': {
return i1 + i2;
}
case '-': {
return i1 - i2;
}
case '*': {
return i1 * i2;
}
}
throw new RuntimeException();
}
// 우선순위 배열로부터 우선순위 가져옴
int getPriority(char[] priority, String now) {
for (int i = 0; i < 3; i++) {
if (priority[i] == now.charAt(0)) return i;
}
return -1;
}
}
결과
- 풀이시간 : 2시간 초과
리뷰
연산 순서를 정렬하는 로직을 구현하면서 컴퓨터의 연산 과정을 이해하는 데에도 도움이 되는 좋은 문제인 것 같습니다.
후위 표기로 변환 후 계산하는 방법을 전에도 배웠는데, 오랜만에 접하니 생각보다 구현이 오래 걸렸습니다. 머릿속 로직을 구현하는 연습을 좀 더 해야할 것 같습니다.
References
| URL | 게시일자 | 방문일자 | 작성자 |
|---|---|---|---|
| 중위 표기(InFix) | 2024.10.01. | 2024.12.18. | Wikipedia |
| 후위 표기(PostFix) | 2024.06.04. | 2024.12.18. | Wikipedia |