출처
접근
규칙을 알고 나면 구하기 쉽지만, 모르면 생각보다 까다로운 문제입니다.
규칙 구하기
주어진 예시 (w = 8, h = 12)에 대해 규칙을 확인해보겠습니다.
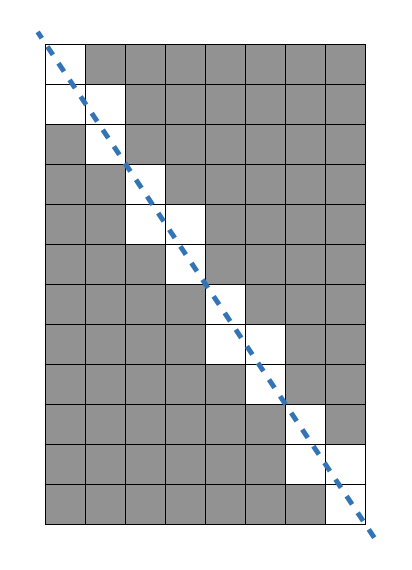
- 문제의 예시를 자세히 보면 작은 사각형이 반복되는 것을 알 수 있습니다.
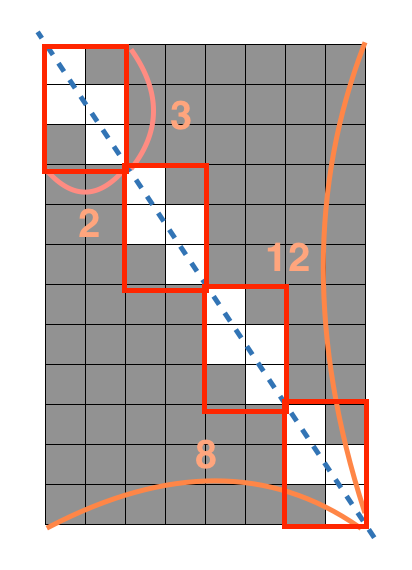
w = 8과h = 12의 최대공약수인4개의 사각형이 생성됩니다.
즉, 최대공약수로 해당 길이를 나누었을 때 생성된 작은 사각형의 잘린 개수를 구하면 됩니다.
최대공약수로 나눠진 사각형(
nw x nh = 2 x 3)의 잘린 개수는 다음과 같이 구할 수 있습니다.
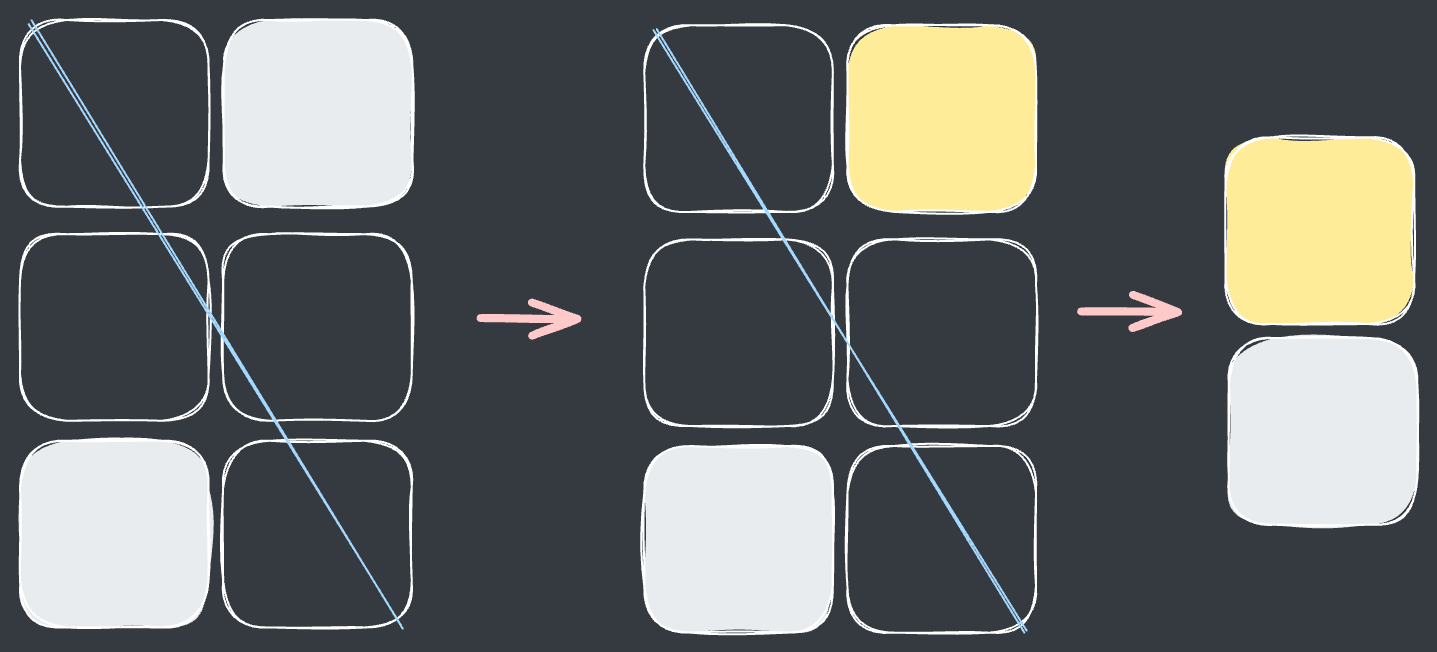
잘리지 않은 사각형을 자른 선 기준으로 구분합니다.(위 : 노랑, 아래 : 하양)
잘리지 않은 사각형끼리 직사각형 형태로 모읍니다.
잘리지 않은 사각형의 크기는 기존 사각형보다 1씩 작은 크기가 됩니다.
남은 사각형 : (nw - 1) x (nh - 1) = 1 x 2다른 형태의 사각형을 여러 개 그려보면서 잘라보면 해당 규칙을 쉽게 발견할 수 있습니다.1
따라서 전체 잘린 사각형의 크기는 다음과 같이 구할 수 있습니다.
잘린 사각형 = 나눠진 사각형 - 잘리지 않은 사각형= (nw x nh) - (nw - 1) * (nh - 1)= (nw * nh) - (nw * nh - nw - nh + 1)= (nw + nh - 1)
유클리드 호제법
유클리드 호제법은 최대공약수를 빠르게 구할 수 있는 알고리즘입니다.
정수
a, b에 대하여 두 수의 최대공약수를(a, b)라고 표현하면 아래 식이 성립합니다.(a, b) = (b, a % b)
증명은 위 위키백과 링크에 자세히 정리되어 있으니 필요하시면 참고하시기 바랍니다!
위 문제의 예시에서
w = 8, h = 12이므로, 두 수의 최대공약수를 다음과 같이 구할 수 있습니다.(8, 12) = (8, 12 % 8) = (8, 4)(8, 4) = (8 % 4, 4) = (0, 4)∴ (8, 12) = 4위 과정을 일반화하여 코드로 나타내면 다음과 같이 재귀적으로 표현할 수 있습니다.
int getGcd(int w, int h) { // 피제수가 0이면 나머지 숫자가 최대공약수 if (h == 0) return w; // 유클리드 호제법으로 재귀호출 return getGcd(h, w % h); }
나머지 연산 과정에서 최대
log(N)씩 피제수가 감소하므로, 시간복잡도는O(log N)가 됩니다.
풀이
- 소요시간 : 1:08:00
class Solution {
public long solution(int w, int h) {
int d = getGcd(w, h);
int nw = w / d, nh = h / d;
return (long)w * h - (nw + nh - 1) * d;
}
int getGcd(int w, int h) {
if (h == 0) return w;
return getGcd(h, w % h);
}
}
결과
- 소요 시간 : 01:08:53
리뷰
규칙을 구하는데 너무 오래 걸렸고, 유클리드 알고리즘도 오랜만에 쓰려다 보니 생각이 안나서 위키백과를 참고했습니다.
유클리드 알고리즘을 모르면 시간복잡도 내 풀 수 없는 문제들도 있으니, 만날 때마다 한번씩 사용해보는게 중요한 것 같습니다.
References
| URL | 게시일자 | 방문일자 | 작성자 |
|---|---|---|---|
| 유클리드 호제법 | 2024.10.22 | 2024.12.23. | Wikipedia |
3 x 4, 3 x 5, 4 x 5인 사각형 중 잘리지 않은 크기는 다음과 같습니다.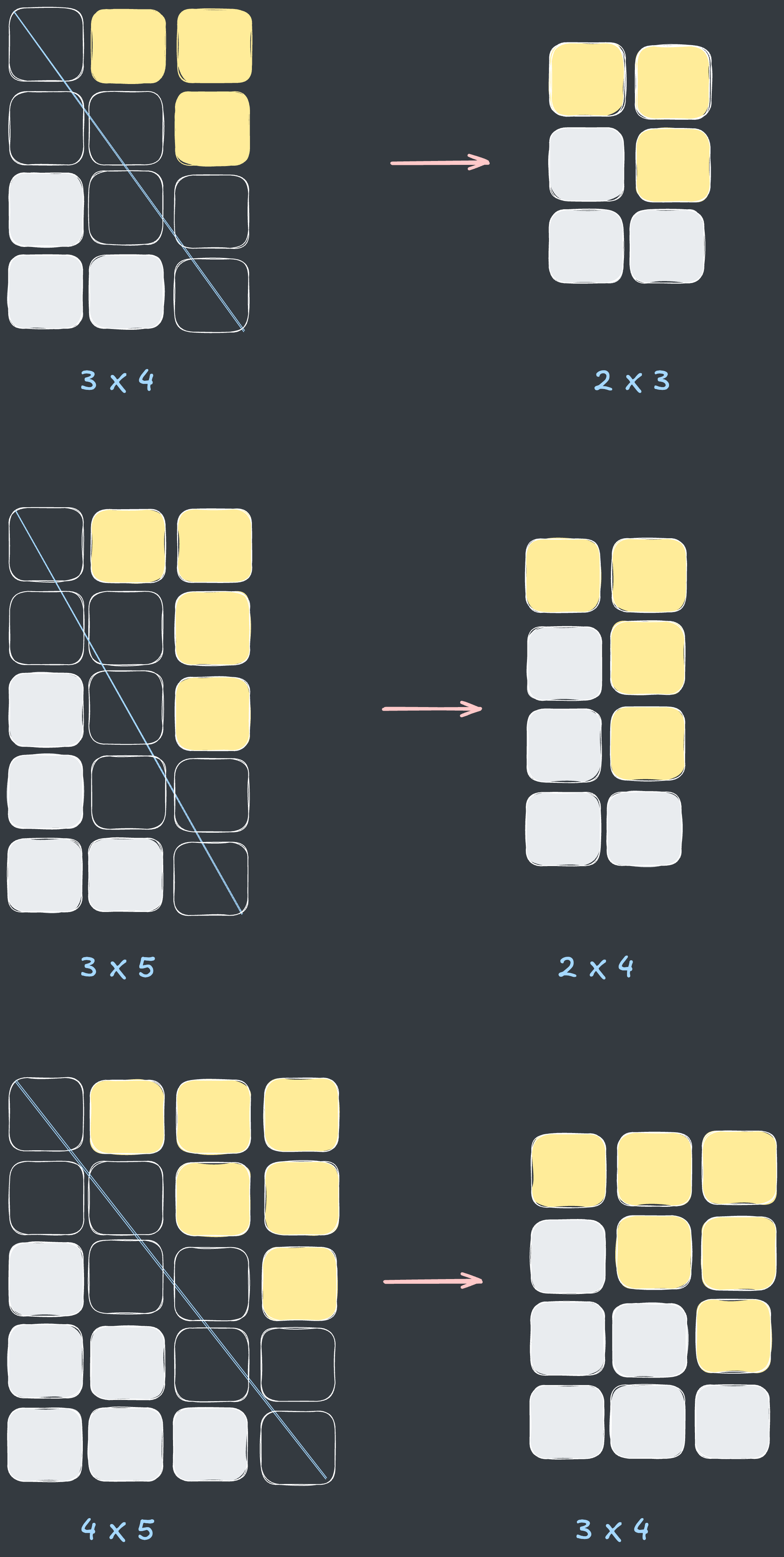 ↩︎
↩︎