출처
접근
문제 분석
- 알파벳 순으로 정렬된 주문서에서 주어진 숫자(
n)에 해당하는 주문서를 찾는 문제입니다. - 이 때, 특정 주문(
bans)이 삭제되어 있는 상태입니다.
시간복잡도 분석
- 주어진 숫자는
n = 10^15인 long 타입의 숫자입니다.
따라서 해당 숫자에서 글자를 가져오는 알고리즘은
O(N)보다 작아야 합니다.
- 주어진 주문인
bans는 길이가300,000이하입니다. 또한, 각 주문의 길이는 최대11입니다.
모든 주문의 알파벳을 비교하기 위해서는
300,000 x 300,000(주문 간 비교) x 11(주문 길이)= 9x10^12 x 11이므로 시간복잡도가 초과될 가능성이 있습니다. 따라서 전체 주문을 최대O(NlogN)까지 확인할 수 있습니다.
공간복잡도 분석
- 문제에서 삭제된 주문이 주어지기 때문에 이를 별도로 저장할 필요는 없습니다.
풀이
26진법
- 주문서의 순서는 다음과 같습니다.
"a"→"b"→"c"→"d"→"e"→"f"→...→"z"
→"aa"→"ab"→...→"az"→"ba"→...→"by"→"bz"→"ca"→...→"zz"
→"aaa"→"aab"→...→"aaz"→"aba"→...→"azz"→"baa"→...→"zzz"
→"aaaa"→...→"aazz"→"abaa"→...→"czzz"→"daaa"→...→"zzzz"
→"aaaaa"→...
- 위와 같은 형태는 26진법과 동일합니다.
주어진 숫자를 뒤에서부터 26으로 나누면서 확인하면 문자(주문)로 변경할 수 있습니다.
봉인된 주문배열 정렬
- 문제에서 주어지는 봉인된 주문의 배열인
bans는정렬 후 확인해야 합니다.
작은 값부터 확인하는 이유는 앞에서 제거한 주문이 이후의 결과에 영향을 줄 수 있기 때문입니다.
- 문제의 1번 예제를 통해 정렬해야 하는 이유를 확인해보겠습니다.
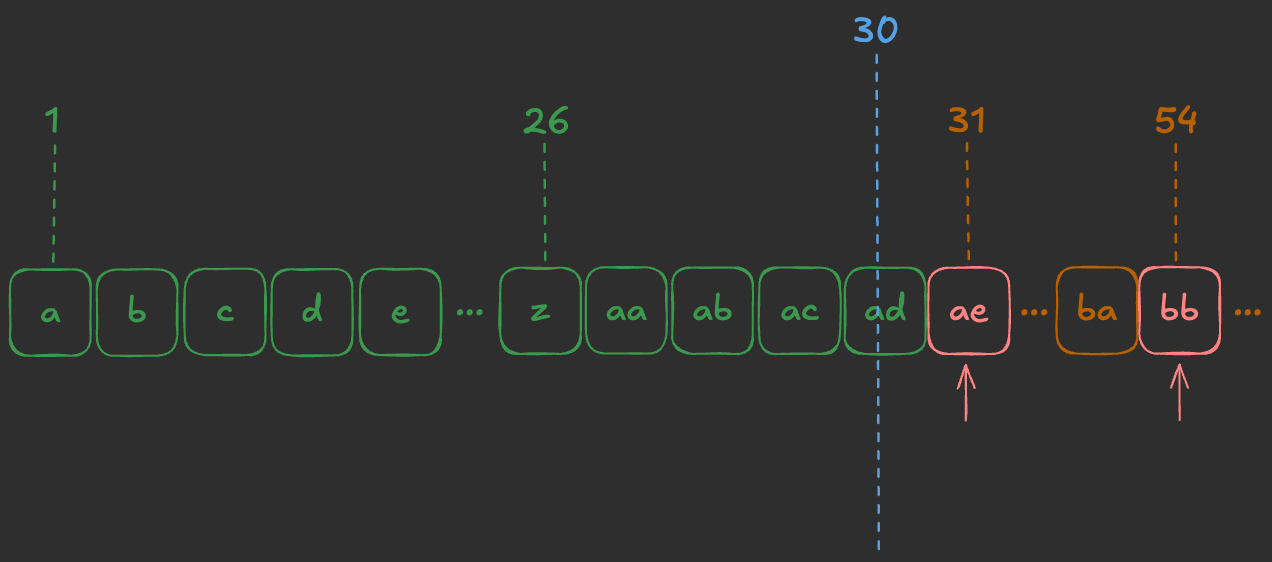
- 위와 같이
ae라는 주문이 먼저 나오게 되면, 문제에서 주어진n = 30보다 크기 때문에 해당 주문은 무시해야 합니다.
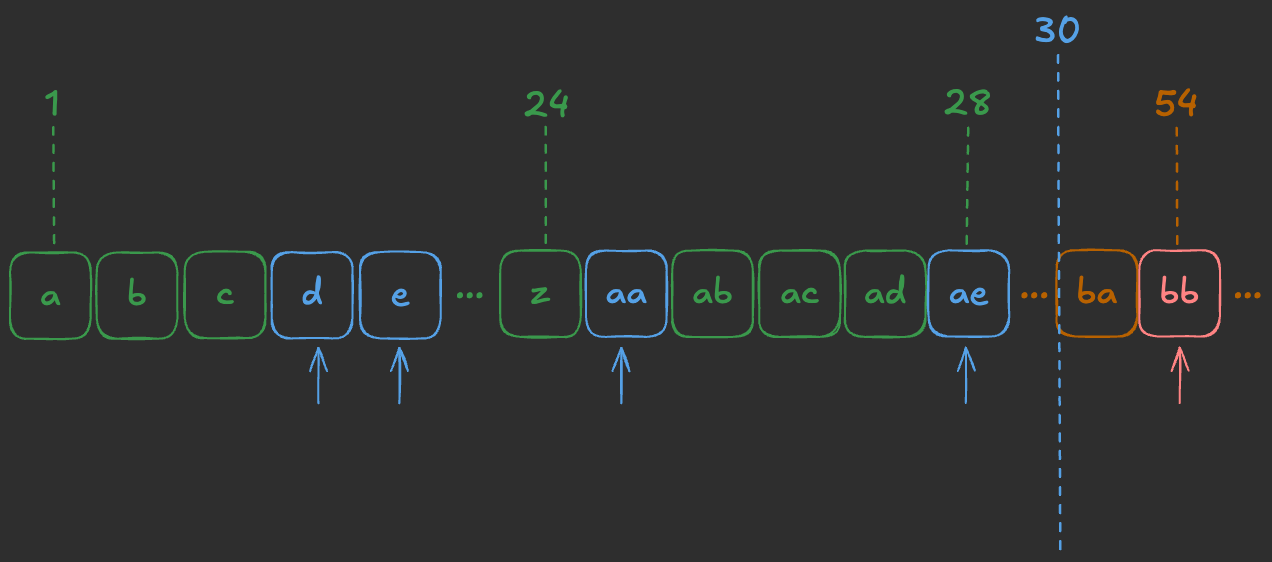
- 그러나, 위와 같이 앞에서
d, e, aa라는 주문을 제외한 뒤ae라는 주문이 나오면 문제에서 주어진n = 30이 뒤로 밀려나면서 해당 주문을 포함시켜야 합니다.
따라서, 주어진 주문을 앞에서부터 확인하기 위해 정렬이 필요함을 알 수 있습니다.
비교 함수 구현
- 비교함수를 구현하면
정렬할 때와,현재 주문과 삭제된 주문의 크기를 비교할 때 용이합니다.
코드
import java.util.*;
class Solution {
public String solution(long n, String[] bans) {
// 정렬을 통해 삭제된 주문 순서대로 확인
Arrays.sort(bans, (o1, o2) -> compare(o1, o2));
// 삭제된 주문이 현재 주문보다 크다면 주문 숫자 1 증가(삭제 처리)
for (String ban : bans) {
if (compare(ban, getSpell(n)) <= 0) n++;
}
// 최종 주문 반환
return getSpell(n);
}
// 주문 간의 크기 비교
int compare(String s1, String s2) {
// 두 주문의 길이가 다르다면, 길이가 긴 주문이 더 큼
if (s1.length() != s2.length())
return Integer.compare(s1.length(), s2.length());
// 두 주문의 길이가 같다면, 앞에서부터 각 주문의 문자 비교
for (int i = 0; i < s1.length(); i++) {
if (s1.charAt(i) < s2.charAt(i)) return -1;
else if (s1.charAt(i) > s2.charAt(i)) return 1;
}
// 모든 비교가 끝났다면 동일한 주문으로 판단
return 0;
}
// 숫자 -> 주문 변환(진법 변환)
String getSpell(long n) {
StringBuilder sb = new StringBuilder();
// 해당 숫자 맨뒤에서부터 26으로 나눈 값 문자로 치환
while(n > 0){
sb.append((char)('a' + (n - 1) % 26));
n = (n - 1) / 26;
}
// 뒤에서부터 확인했으므로 뒤집기
return sb.reverse().toString();
}
}
결과
리뷰
- 처음부터 진법문제로 생각했다면 훨씬 쉽게 풀었을텐데, 단순 구현이라고 생각해서 복잡한 코드1를 작성하느라 시간이 많이 걸렸습니다.
문제의 본질을 파악하는 습관을 들여야겠습니다.
References
| URL | 게시일자 | 방문일자 | 작성자 |
|---|
최초에 작성한 숫자 -> 문자열 변환 코드입니다. 진법 문제로 생각하지 않고, 각 자리수를 일일이 분리해서 문자열을 찾았습니다.
↩︎String getSpell(long n) { int exp = 0; long start = -1, end = 0; while (end < n) { start += (long)Math.pow(26, exp); end += (long)Math.pow(26, exp + 1); exp++; } StringBuilder sb = new StringBuilder(); while (exp > 0) { long ns = start; int cnt = 0; while (true) { ns += (long)Math.pow(26, exp - 1); if (ns >= n) break; start = ns; cnt++; } sb.append((char)(cnt + 'a')); exp--; } return sb.toString(); }