[Java]Programmers GPS(2017 카카오코드 본선)

출처

• 프로그래머스 GPS(2017 카카오코드 본선)

접근

문제 분석

오류가 발생한 택시의 경로를 최소한으로 수정하여 정확한 이동 경로를 구하는 문제입니다.

• 우선, 택시의 이동을 표현하기 위한 그래프 구조가 필요합니다.
• 문제에서 최소한으로 이동하는 경로를 찾기 위해서는 갈 수 있는 모든 경로에 대해 완전탐색을 수행해야 합니다.

시간복잡도 분석

완전탐색

전체 경우의 수를 BFS 또는 DFS를 활용해서 제한시간 내 목적지까지 갈 수 있는 모든 경로를 찾아서 주어진 경로와의 차이를 비교하는 방법이 있습니다.

• 이러한 경우, 한 거점에서 다음 거점으로 이동하는 경우의 수는 정점과 연결된 간선(m)만큼 곱해지게 됩니다.

정점(n = 200)과 간선(m = 10,000)이 균일하게 연결된 그래프로 가정하면 한 정점에 연결된 간선의 수가 50개이기 때문에, 전체 경우의 수는 정점 1개에 50개씩 증가하여 O(N) = 50 ^ 200이 됩니다.

• 따라서, 단순한 완전탐색으로는 전체 경우의 수를 모두 확인할 수 없음을 알 수 있습니다.

완전탐색을 최적화하는 기법이 필요함을 알 수 있습니다.

풀이

DP

문제의 요구사항은 도착 지점까지 수정한 오류의 개수의 최솟값을 구하는 것입니다.

• 즉, 위의 완전탐색에서 모든 경로를 탐색하는 것은 불필요하며, 각 거점에서 수정한 오류의 최솟값을 알 수 있다면 다음 거점에서의 최솟값을 구할 수 있습니다.

이전 값을 다음 탐색에 활용하는 DP 알고리즘을 적용할 수 있습니다.

문제의 예시를 통해 살펴보겠습니다.

• t = 2일 때 2번 거점의 오류수정 횟수의 최솟값을 구해보겠습니다.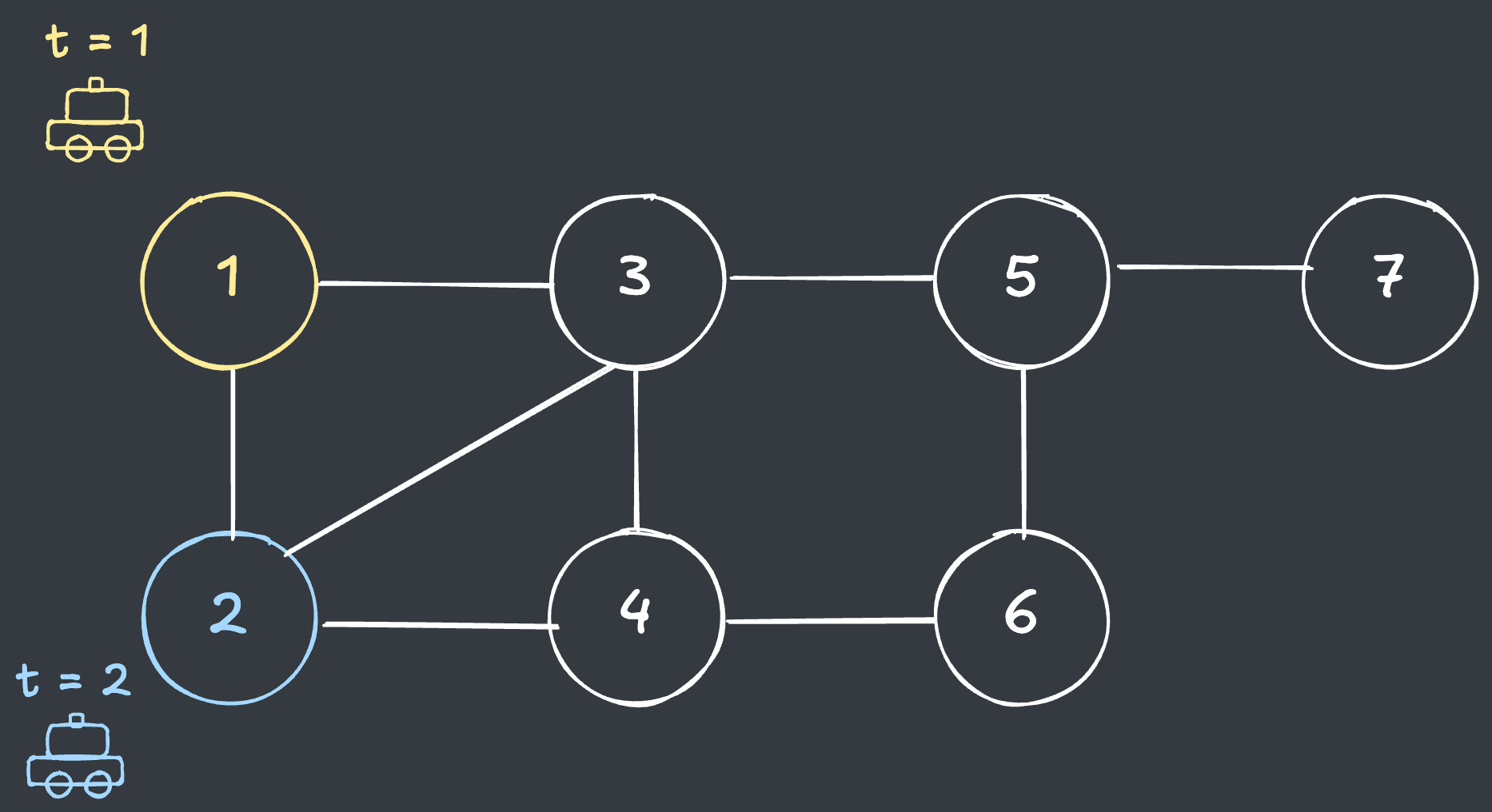

  

  • 문제에서 주어진 택시 경로 상, t = 2일 때 택시는 원래 2번 거점에 있어야 합니다.
  • 따라서 2번 거점은 1번 거점에서 오류수정 없이 이동이 가능합니다.

  문제에서 주어진 경로에 있는 정점은 이전 위치의 값을 그대로 사용할 수 있습니다.

• 이번에는 t = 2일 때 3번 거점의 오류수정 횟수의 최솟값을 구해보겠습니다.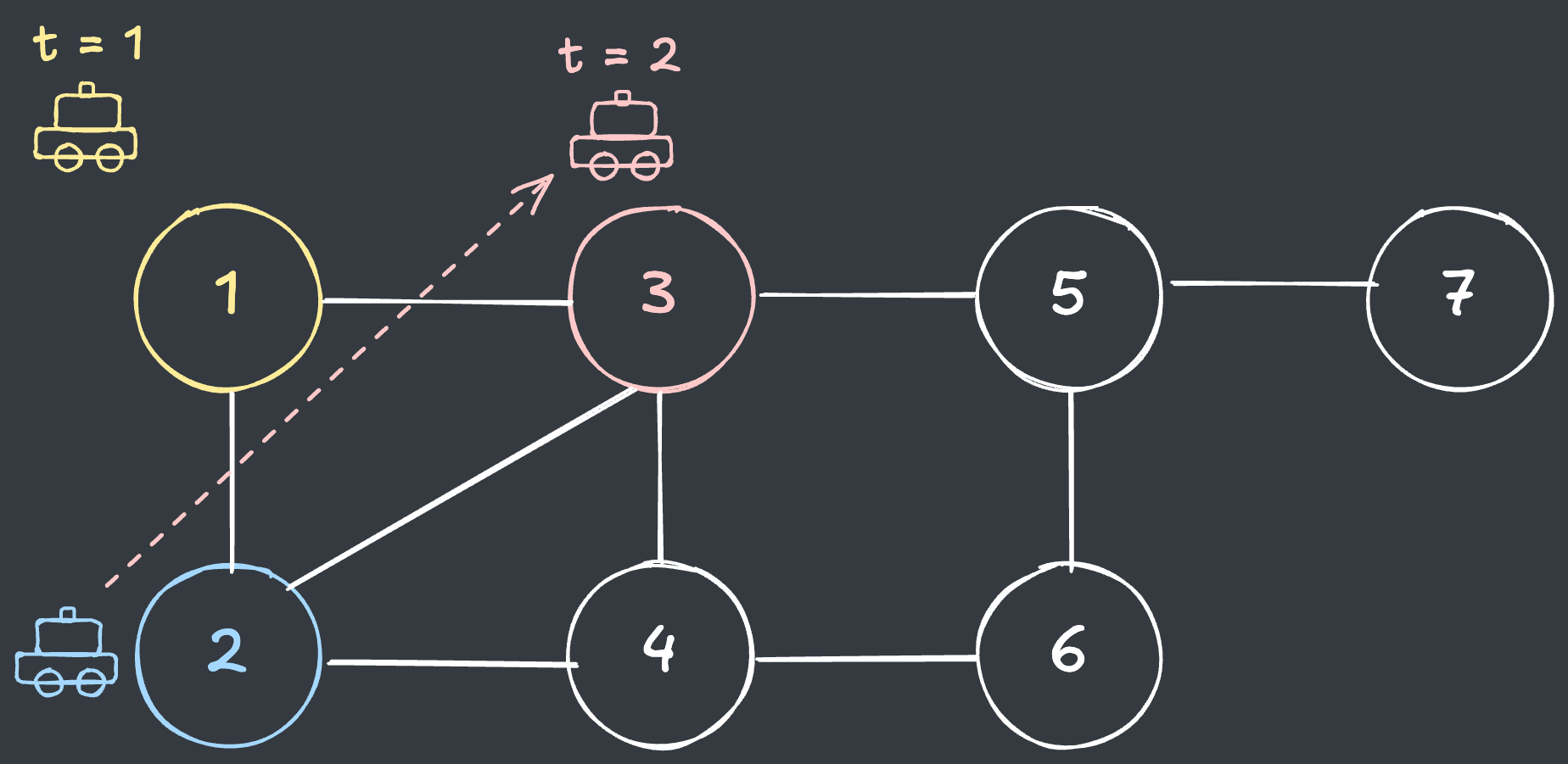

  

  • 문제에서 주어진 택시 경로 상, t = 2일 때 택시는 원래 2번 거점에 있어야 합니다.
  • 따라서 3번 거점은 1번 거점에서 1회 오류수정을 해야 이동할 수 있습니다.

  문제에서 주어진 경로가 아닌 정점은 이전 위치의 값에서 오류수정이 1회 필요합니다.

• 이번에는 t = 2일 때 1번 거점의 오류수정 횟수의 최솟값을 구해보겠습니다.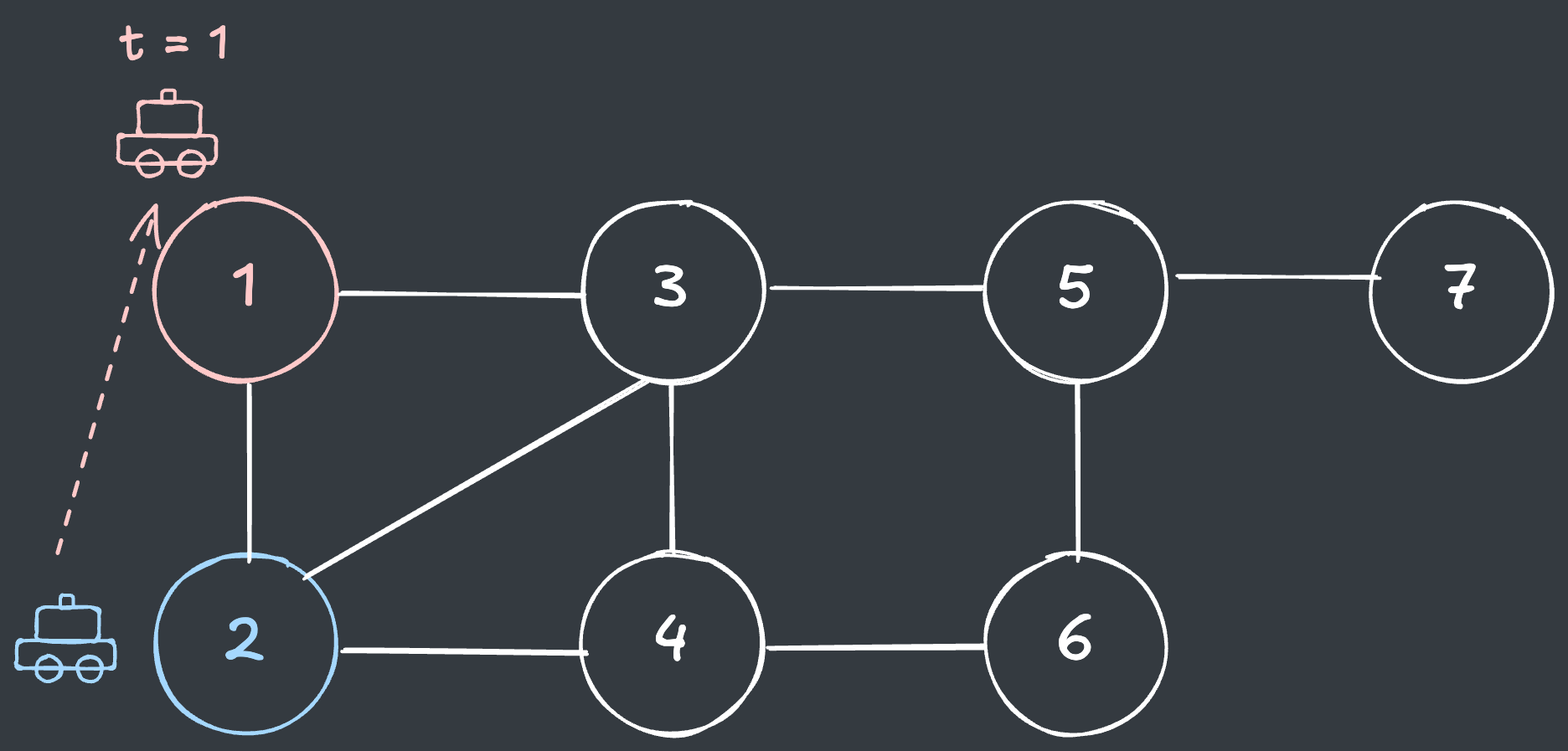

  

  • 문제에서 주어진 택시 경로 상, t = 2일 때 택시는 원래 2번 거점에 있어야 합니다.
  • 따라서 1번 거점은 1번 거점에서 1회 오류수정을 해야 이동할 수 있습니다.

  택시가 이전 위치에 그대로 있는 경우도 있음을 유의합니다.

규칙성을 좀 더 명확히 찾기 위해 t = 3인 상황을 확인해보겠습니다.

• t = 3일 때 1번 거점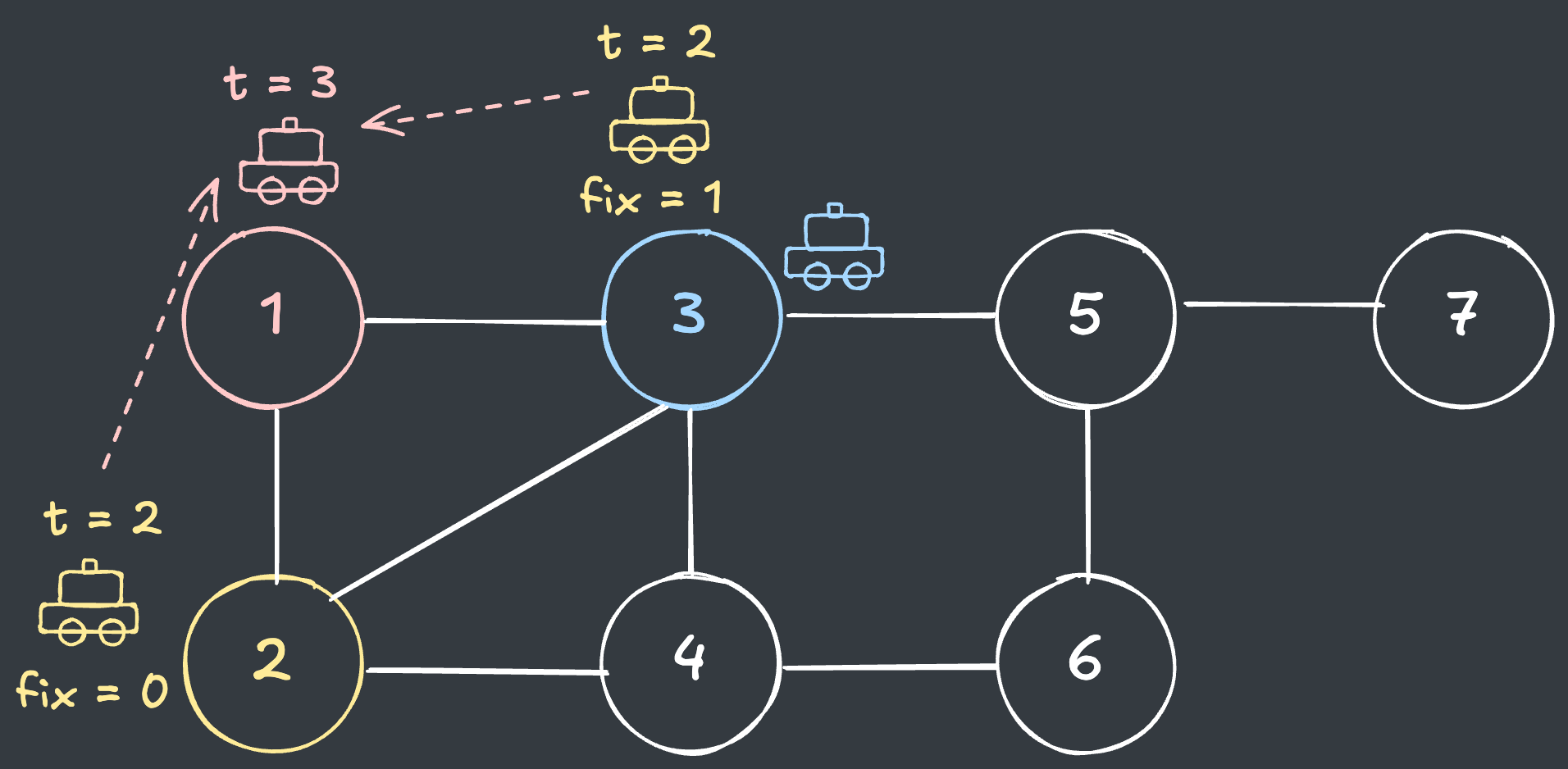

  

  • t = 3일 때 택시는 원래 3번 거점에 있어야 합니다.(오류수정 1회 필요)
  • 1번 거점에서 이동 시 : t = 2일 때 1번 거점의 값인 1 + 오류수정 1회 => 2
  • 2번 거점에서 이동 시 : t = 2일 때 2번 거점의 값인 0 + 오류수정 1회 => 1
  • 3번 거점에서 이동 시 : t = 2일 때 3번 거점의 값인 1 + 오류수정 1회 => 2

  문제에서 최솟값만 필요하기 때문에, 2번 거점에서 1번 거점으로 이동하는 1만 저장합니다.

위와 같은 방식으로 특정 시간에 특정 거점의 오류수정 횟수의 최솟값을 DP에 저장하여 완전탐색을 최적화할 수 있습니다.

오류수정으로 도달할 수 없는 경우 -1을 반환해야 함을 주의합니다.

코드

import java.util.*;

class Solution {
    public int solution(int n, int m, int[][] edge_list, int k, int[] gps_log) {

        // 그래프(간선 리스트) 생성
        List<Integer>[] adjList = new List[n + 1];
        for (int i = 0; i < m; i++) {
            int from = edge_list[i][0], to = edge_list[i][1];
            if (adjList[from] == null) adjList[from] = new ArrayList<>(List.of(from));
            if (adjList[to] == null) adjList[to] = new ArrayList<>(List.of(to));
            adjList[from].add(to);
            adjList[to].add(from);
        }

        // DP 생성 및 초기화 : i : 시간, j : 거점, DP[i][j] -> 'i'시간에 'j'거점에 도착할 수 있는 최소 오류수정 횟수 
        int[][] dp = new int[k][n + 1];
        Arrays.stream(dp).forEach(d -> Arrays.fill(d, Integer.MAX_VALUE));
        dp[0][gps_log[0]] = 0;

        // DP 완전탐색
        for (int i = 1; i < k; i++) {
            for (int j = 1; j <= n; j++) {

                // 이전 거점이 도달할 수 없는 위치이면 통과
                if (dp[i - 1][j] == Integer.MAX_VALUE) continue;

                // 간선리스트 탐색
                for (int next : adjList[j]) {

                    // 택시 경로에 위치한 경우 : 이전 경로 값의 최솟값 사용
                    if (next == gps_log[i]) dp[i][next] = Math.min(dp[i][next], dp[i - 1][j]);

                        // 택시 경로에 위치하지 않은 경우 : 이전 경로 값의 최솟값 + 1 사용
                    else dp[i][next] = Math.min(dp[i][next], dp[i - 1][j] + 1);
                }
            }
        }

        // 마지막 거점의 최소 오류수정 횟수 반환
        int answer = dp[k - 1][gps_log[k - 1]];

        // 도달할 수 없으면 -1 반환
        return answer == Integer.MAX_VALUE ? -1 : answer;
    }

}

결과

• 소요시간 : 1시간 초과 + 풀이 검색

리뷰

최단경로(BFS)로 풀어보다가 문제의 테스트 케이스가 1개밖에 없어서 헤매다가 결국 공식 풀이를 일부 참고했습니다.

DP 문제는 다양한 유형을 접해보는 수밖에 없는 것 같습니다.

References