출처

접근

문제 분석

  • 산의 봉우리까지 이동하는 과정을 시뮬레이션 하는 문제입니다.
  • Intensity는 이동 과정에서 가장 긴시간을 뜻합니다.
  • 문제에서는 정상에 도착한 후, 다시 출입구로 돌아와야 한다고 했지만 올라갔던 길을 그대로 내려올 수 있기 때문에, 정상까지만 경로를 추적하면 됩니다.
  • 따라서 각 출발지(Gate)에서 도착지(Summit)까지의 Intensity가 최소가 되도록 완전탐색을 수행해야 합니다.

조건 분석

  • 문제에서 주어진 정점(Vertex)은 n = 50,000 이고 간선(Edge)은 paths = 200,000입니다.
  • 탐색의 시작점이 최대 n이기 때문에, 각 간선을 1번씩만 방문하도록 최적화하면 시간복잡도 내 문제를 해결할 수 있습니다.

    O(N) = n + paths = 250,000

  • 이 때, 정점의 개수에 비해 간선이 적으므로, 인접 리스트를 활용하는 것이 효과적입니다.1

    간선의 개수가 적은 그래프에서 행렬(n x n matrix)을 사용하게 되면, 불필요한 탐색 및 메모리 초과가 발생할 수 있습니다.

BFS

  • 한 정점에서 다른 정점으로 이동 시, 깊이를 따라 이동하면(DFS) 불필요한 탐색이 발생하기 때문에 시간초과가 발생할 수 있습니다.

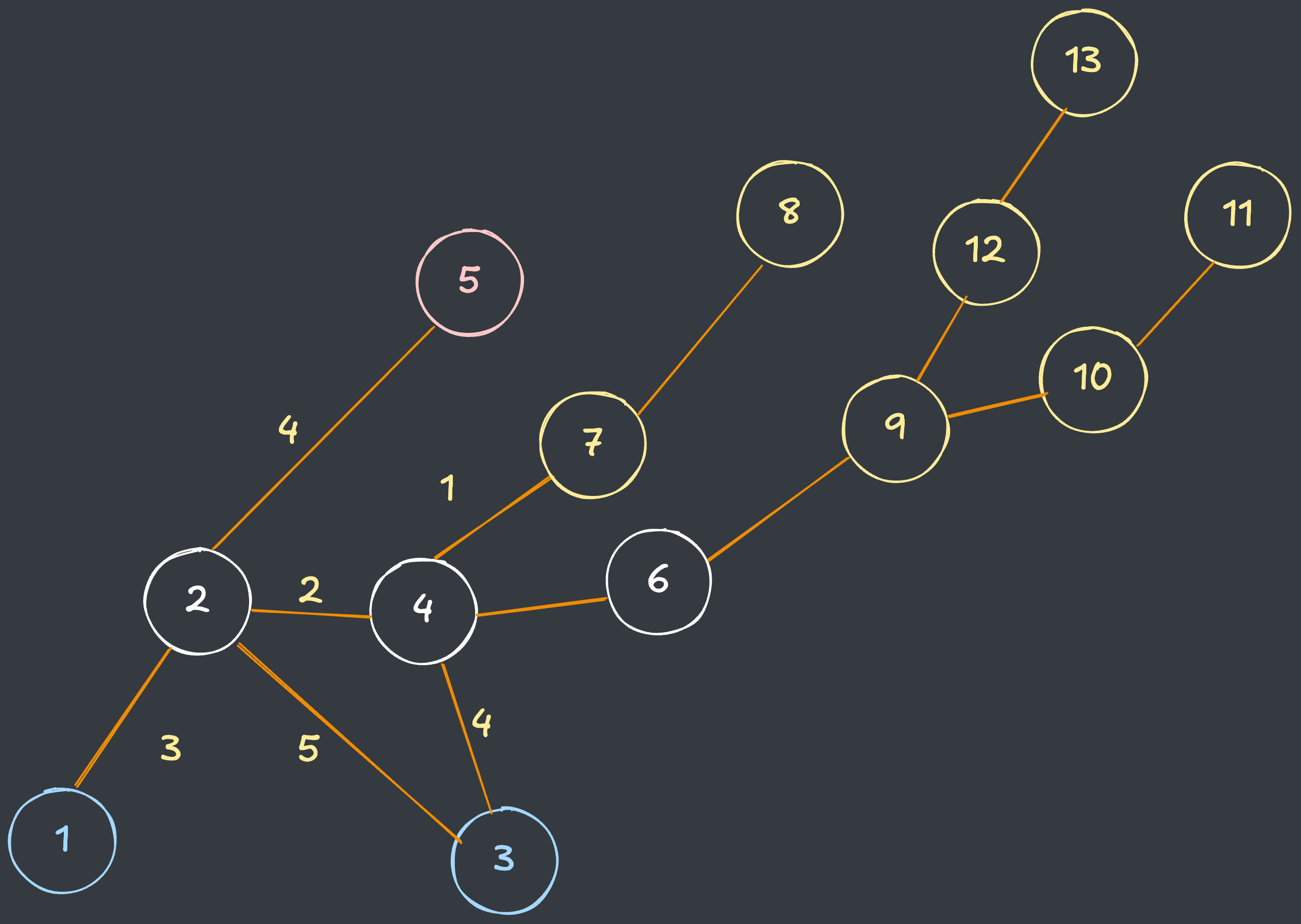
    • 아래와 같은 깊은 그래프가 있다고 가정하겠습니다. img_3.png

    • DFS는 산꼭대기에 도착할때까지 깊이가 계속 깊어지므로, 다음과 같이 깊은 그래프에서는 모든 경로를 탐색하면서 시간복잡도가 계속 증가하게 됩니다.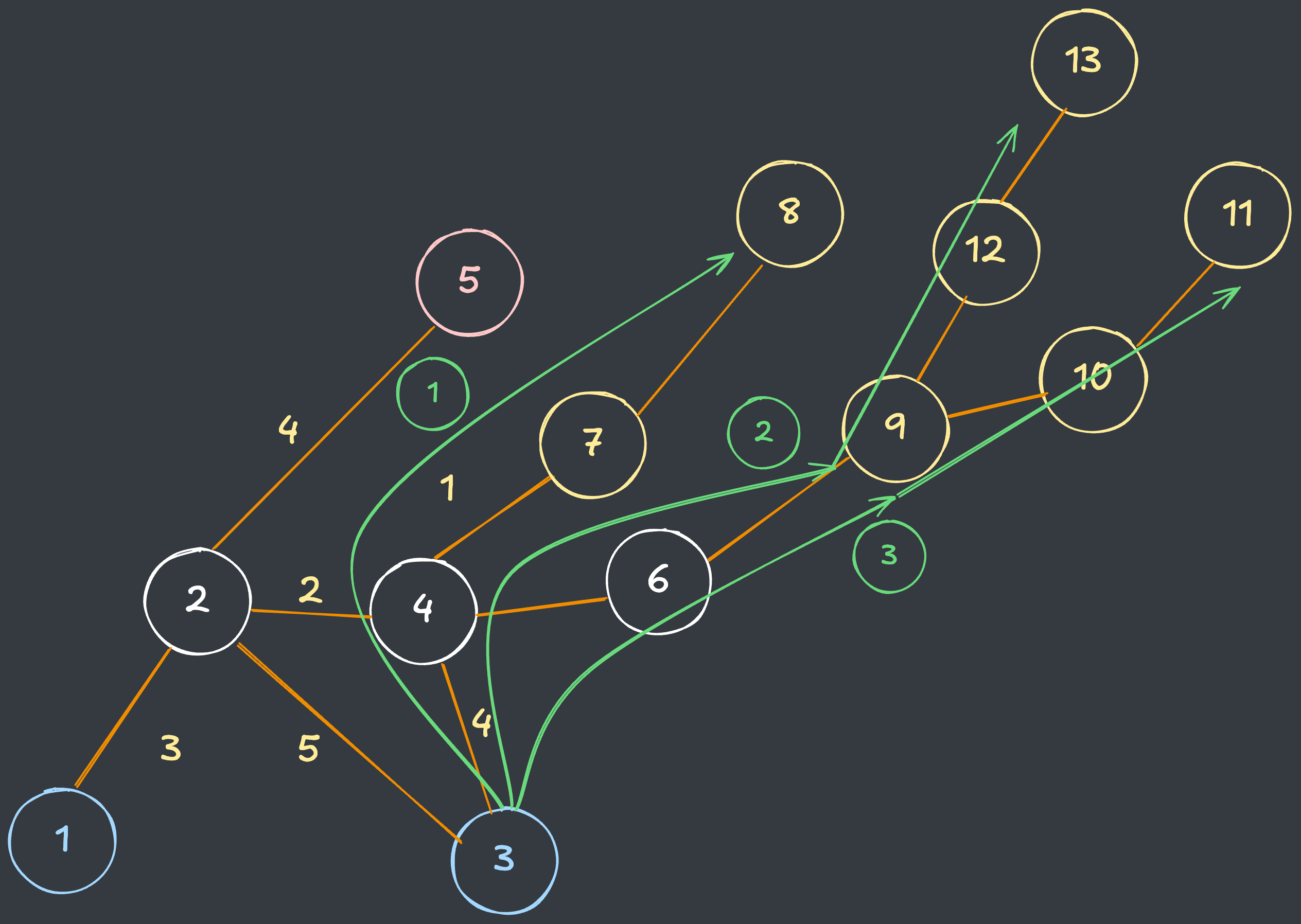 img_2.png

    • 그러나 BFS에서는 최단 경로로만 이동하기 때문에 불필요한 탐색을 최적화할 수 있습니다.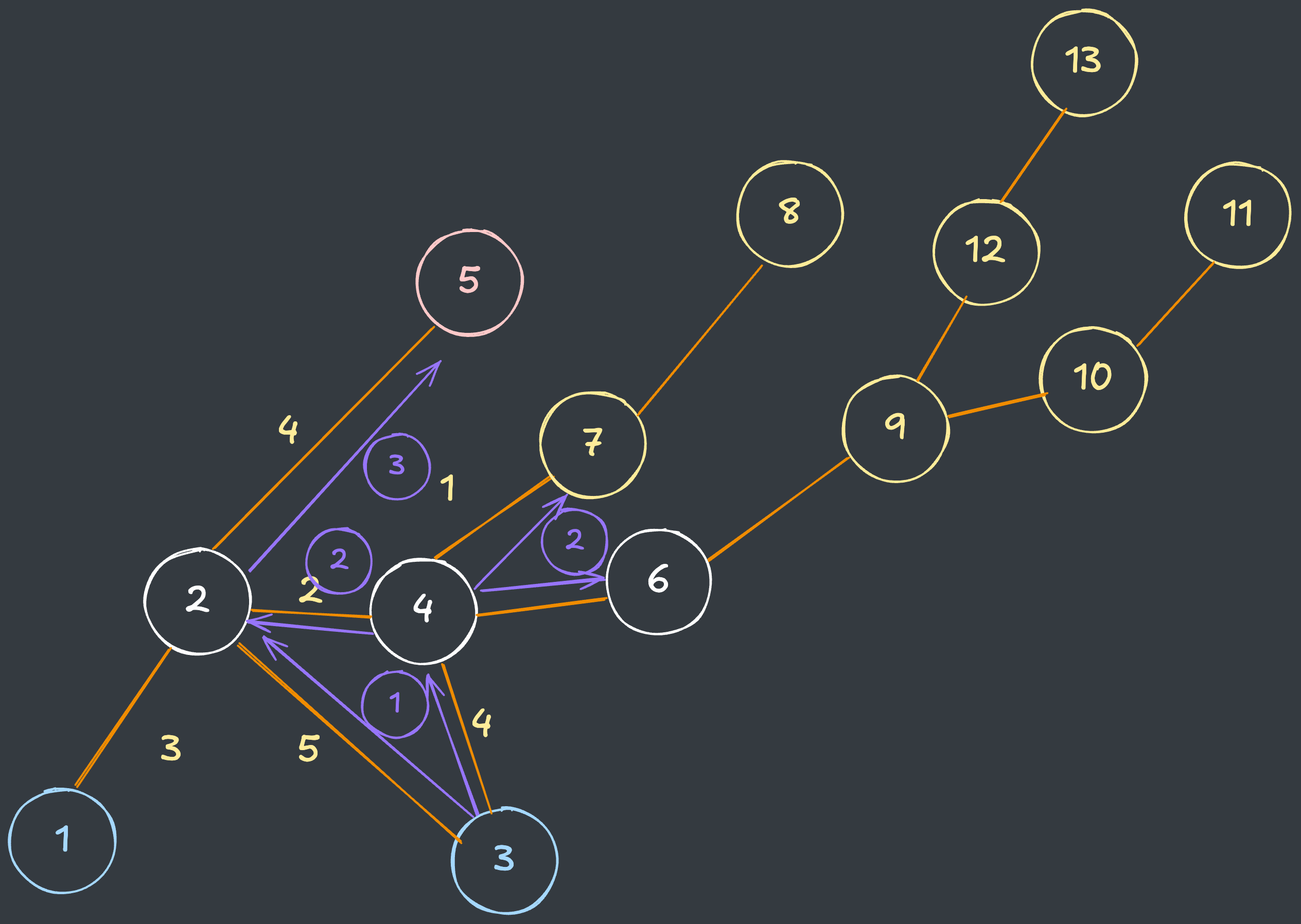 img_4.png

방문처리 최적화

  • 단순히 방문여부로 방문체크를 한다면, 이후에 더 작은 Intensity로 방문하는 경우를 탐색할 수 없기 때문에, 방문처리 배열은 DP 형태로 Intensity 최솟값을 저장해야 합니다.

  • 문제에서 주어진 시작점이 여러개이기 때문에, 새로운 시작점에서 서로 다른 BFS를 수행하게 됩니다.

  • 그러나, 이전 등산코스에서 방문했던 지점이라면, 새로운 BFS에서 다시 방문할 필요가 없기 때문에 이를 최적화할 수 있습니다.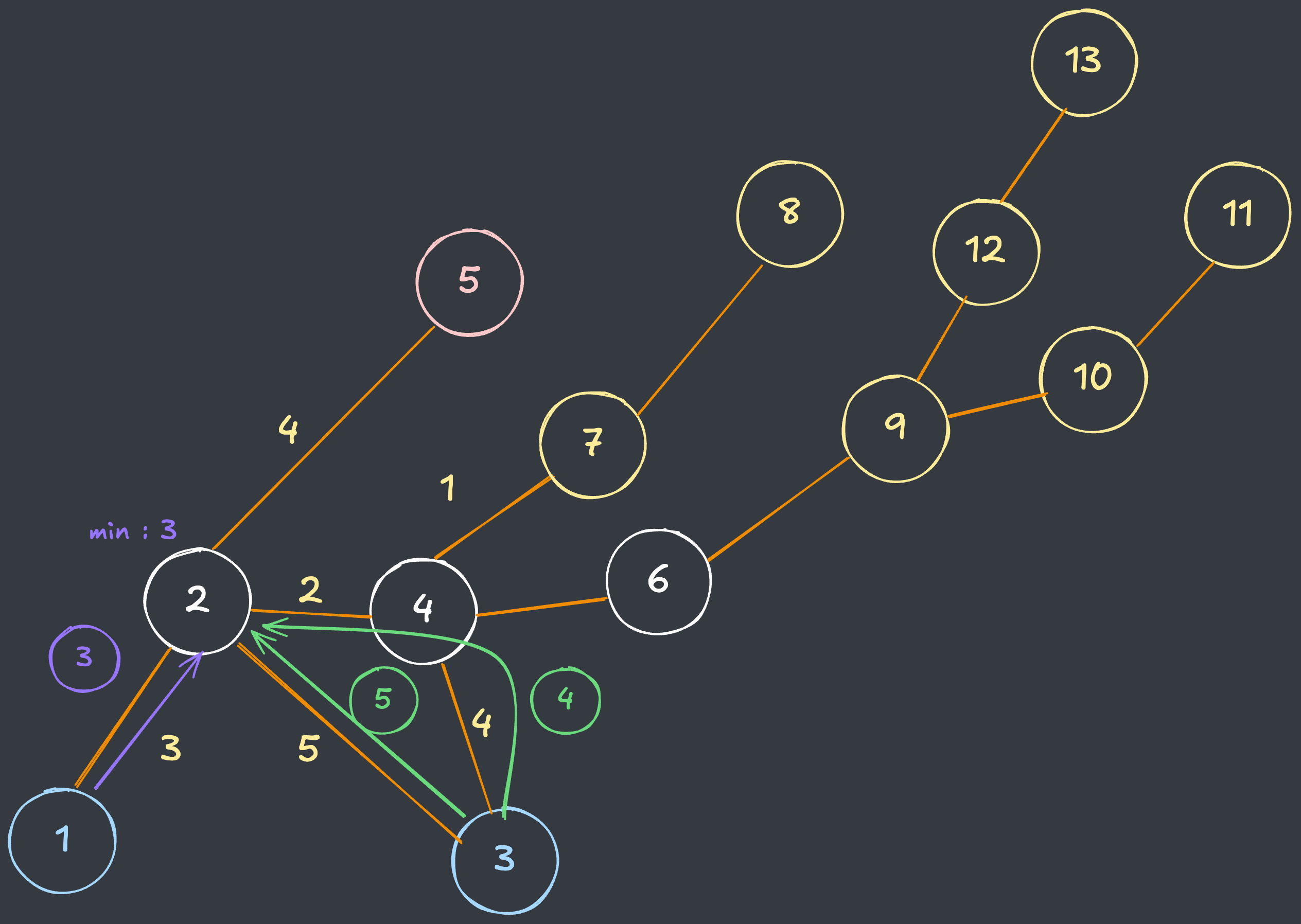

    img_5.png

    • 위와 같이 1번 시작점에서 Intensity = 3으로 방문했던 지점이라면, 3번 시작점에서는 어떻게 해도 Intensity를 줄일 수 없기 때문에 해당 정점은 더이상 방문할 필요가 없습니다.

  • 더 나아가서, 탐색 과정에서 해당 정점을 이미 더 작은 가중치로 다시 방문할 필요가 없기 때문에 최적화가 가능합니다.

최소 가중치만 방문하는 점에서 다익스트라 알고리즘이 됩니다.

도착지 최적화

  • 도착지를 Set에 삽입하면, 해당 지점이 도착지인지 O(1)로 판단할 수 있기 때문에 도착여부를 빠르게 파악할 수 있습니다.
  • 이 때, 문제에서 산봉우리 번호가 더 낮은 등산코스를 선택해야 하기 때문에, 더 빠른 도착지점이 앞으로 올 수 있도록 TreeSet으로 구현체를 선택합니다.

TreeSet은 내부 원소를 정렬된 형태로 유지합니다.

풀이

import java.util.*;

class Solution {
    // 정답 초기화
    int[] answer = {0, 10_000_001};
    
    public int[] solution(int n, int[][] paths, int[] gates, int[] summits) {
        
        // 인접리스트 정의 및 생성
        List<int[]>[] adjList = new List[n + 1];
        for (int i = 0; i < paths.length; i++) {
            
            int start = paths[i][0], end = paths[i][1], time = paths[i][2];
            
            if (adjList[start] == null) adjList[start] = new ArrayList<>();
            if (adjList[end] == null) adjList[end] = new ArrayList<>();
            
            adjList[start].add(new int[] {end, time});
            adjList[end].add(new int[] {start, time});
        }
        
        // DP 형태의 방문배열
        int[] isVisited = new int[n + 1];
        Arrays.fill(isVisited, 10_000_001);
        
        // 도착지 Set
        Set<Integer> summitSet = new TreeSet<>();        
        for (int summit : summits)
            summitSet.add(summit);
        
        // 각 시작지점에서 다익스트라 수행
        for (int start : gates){          
            dijkstra(n, start, adjList, isVisited, summitSet);
        }
        
        return answer;
    }
    
    void dijkstra(int n, int start, List<int[]>[] adjList, int[] isVisited, Set<Integer> summitSet) {
        
        // Dijkstra를 위한 PriorityQueue
        PriorityQueue<int[]> q = new PriorityQueue<>((o1, o2) -> Integer.compare(o1[1], o2[1]));


        isVisited[start] = 0;
        q.offer(new int[] {start, 0});
        
        while (!q.isEmpty()) {
            int[] now = q.poll();

            // 탐색 과정에서 더 작은 가중치가 발생한 경우 탐색 종료
            if (now[1] > isVisited[now[0]]) continue;
            
            // 도착지점일 경우 탐색 종료
            if (summitSet.contains(now[0])) continue;
            
            for (int[] adjs : adjList[now[0]]) {
                
                // Intensity : 현재 경로에서 가장 긴 시간
                int intensity = Math.max(adjs[1], now[1]);
                
                // 방문체크 : Intensity가 더 작을때만 재방문
                if (intensity >= isVisited[adjs[0]]) continue;
                isVisited[adjs[0]] = intensity;
                                         
                // 새로운 지점에서 다시 BFS
                q.offer(new int[] {adjs[0], intensity});
            }
        }
        
        // 산봉우리의 최솟값 찾기
        int minSummit = 0, minIntensity = 10_000_001;
        
        // TreeSet이므로 번호가 낮은 산봉우리부터 확인
        for (int summit : summitSet) {
            
            // 번호가 큰 산봉우리는 Intensity 최솟값이 작을때만 갱신 
            if (isVisited[summit] < minIntensity) {
                minIntensity = isVisited[summit];
                minSummit = summit;
            }
        }
        
        // 정답 최신화
        if ((answer[1] > minIntensity) ||
            // Intensity가 같으면 번호 확인
            (answer[1] == minIntensity && answer[0] > minSummit)) {
            answer = new int[] {minSummit, minIntensity};
        } 
    }
}

결과

  • 소요 시간 : 1시간 30분

img_7.png

리뷰

  • 문제를 정확히 이해하지 않고 구현하려다 보니 구현이 오래 걸렸습니다.

코스에서 가중치가 가장 작은 값만 확인하면 되므로 일반적인 Dijkstra와는 다른 로직임을 나중에야 알게 되었습니다. 문제를 정확히 이해하고 구현하는 습관을 길러야겠습니다.

References

URL게시일자방문일자작성자
희소 그래프2023.04.01.2025.01.22.Wikipedia

  1. 정점에 비해 간선이 적은 그래프를 희소 그래프라고 합니다.

    해당 문제에서 최대 간선의 숫자는 n * (n - 1) / 2 = 1,249,975,000인 반면, 해당 그래프의 간선의 숫자는 200,000이므로 정점에 비해 간선이 적다고 할 수 있습니다.

     ↩︎