출처
접근
완전탐색(DFS)
자식 방에서 부모(Root) 방향으로 DFS를 하면서 지상에 도달하는데 걸리는 시간을 확인합니다.
- 개미 방의 개수가 최대
10^5이므로, 최악의 경우인 방이 일렬로 나열된 경우를 고려해야 합니다.1선형적인 DFS로는 시간복잡도가 초과할 것이라고 생각해서 BinarySearch로 최적화를 했는데, 선형으로 조상들을 탐색해도 시간초과가 되지 않는 것으로 보아 DFS 만으로도 풀 수 있을 것 같습니다.
TREE + BinarySearch
문제를 다시 읽어보면 자신 부모들의 집합, 즉, 조상들을 하나씩 타고 올라가면서 갈 수 있는 최대 조상의 번호를 반환해야 함을 알 수 있습니다.
조상의 정보를 배열로 저장할 수 있다면, 현재 개미가 가진 에너지로 도달할 수 있는 위치를 이분탐색으로 찾을 수 있습니다.
- 주어진 예제를 다음과 같이 Tree 형태로 그릴 수 있습니다.

예제를 트리 형태로 나타낼 수 있습니다.
- 각 노드에 조상들의 정보를 배열로 저장합니다.

각 노드별로 조상의 정보를 저장합니다.
- 위와 같이 본인을 포함한 자신의 조상들의 정보(
조상노드 번호(num), 다음 부모까지의 거리(dist))를 배열에 저장할 수 있습니다.
예를 들어, 3번 노드는 부모인 2번 노드까지 거리가 10 소요되고, 조상인 1번 노드까지 거리가 20 소요되므로 조상 배열은
[[3, 10], [2, 20], [1, 20]]이 됩니다.
- 최대로 갈 수 있는 조상 번호를 구합니다.

각 노드별로 조상의 정보를 저장합니다.
- 문제에서 주어진 에너지를 통해 본인의 조상 노드 중 최대로 갈 수 있는 노드의 위치를 구합니다.
- 이 때, 조상과의 거리가 오름차순으로 증가하기 때문에, BinarySearch2를 통해 시간복잡도를
O(N) -> O(logN)으로 최적화할 수 있습니다.
테스트케이스에 최악의 시나리오는 없는지 이분탐색을 하지 않아도 시간초과가 발생하지는 않습니다.
풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
// 방 노드 해시맵에 별도로 저장
static Map<Integer, Room> rooms = new HashMap<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
// 개미 에너지 초기화
int[] ants = new int[n + 1];
List<int[]>[] adjList = new List[n + 1];
for (int i = 1; i <= n; i++) {
ants[i] = Integer.parseInt(br.readLine());
adjList[i] = new ArrayList<>();
}
// 간선 리스트 초기화
StringTokenizer st;
for (int i = 1; i < n; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int dist = Integer.parseInt(st.nextToken());
adjList[from].add(new int[]{to, dist});
adjList[to].add(new int[]{from, dist});
}
// DFS로 개미집 초기화
Room root = new Room(1);
rooms.put(1, root);
dfs(root, adjList);
// 각 개미들의 Root 찾기
StringBuilder answer = new StringBuilder();
for (int i = 1; i <= n; i++) {
answer.append(rooms.get(i).getFarRoomLeaner(ants[i]));
answer.append("\n");
}
System.out.println(answer);
}
// DFS로 전체 개미집 구조 생성
static void dfs(Room root, List<int[]>[] adjList) {
Stack<Room> stack = new Stack<>();
boolean[] visited = new boolean[adjList.length];
stack.push(root);
visited[1] = true;
while (!stack.isEmpty()) {
Room cur = stack.pop();
// 부모 집으로부터 자식 집 생성
for (int[] child : adjList[cur.num]) {
if (visited[child[0]]) continue;
visited[child[0]] = true;
Room croom = new Room(child[0], child[1], cur);
stack.push(croom);
rooms.put(child[0], croom);
}
}
}
static class Room {
int num;
Room parent;
int[][] ancestor;
List<Room> children;
Room(int num) {
this.num = num;
this.children = new ArrayList<>();
this.ancestor = new int[][] {{1, 0}};
rooms.put(num, this);
}
// 자식의 조상은 부모 조상에 현재 굴 길이 추가하기
Room(int num, int dist, Room parent) {
this.num = num;
this.parent = parent;
this.ancestor = new int[parent.ancestor.length + 1][2];
this.children = new ArrayList<>();
for (int i = 0; i < parent.ancestor.length; i++) {
// 현재 ~ 부모까지의 거리를 모든 조상 거리에 더해줌
ancestor[i + 1] = new int[] {parent.ancestor[i][0], parent.ancestor[i][1] + dist};
}
// 첫번째 조상에 [자신, 부모까지의 거리] 추가
ancestor[0] = new int[] {this.num, dist};
}
// 선형으로 가장 멀리 떨어진 방 찾기
public int getFarRoomLeaner(int energy) {
for (int[] ints : ancestor) {
if (ints[1] > energy) return ints[0];
}
return ancestor[ancestor.length - 1][0];
}
// 이분탐색으로 가장 멀리 떨어진 방 찾기
public int getFarRoomBinary(int energy) {
int left = 0, right = ancestor.length;
while (left < right) {
int middle = (left + right) / 2;
if (energy < ancestor[middle][1]) {
right = middle;
}
else left = middle + 1;
}
return left == ancestor.length? 1 : ancestor[left][0];
}
}
}
결과
- 소요시간 : 2시간 초과

리뷰
선형탐색도 시간이 충분한데 이분탐색으로 안하면 시간복잡도가 터질 것 같아서 괜히 UpperBound를 구현한다고 더 시간이 걸린 것 같습니다.
플래티넘 문제라서 당연히 시간이 빡빡할거라고 생각했는데… 과한 최적화는 역시 항상 주의해야겠습니다.
References
| URL | 게시일자 | 방문일자 | 작성자 |
|---|
방이 일렬이라고 가정하면, 다음과 같이 최악의 경우에 Depth가
10^5인 DFS를 수행해야 합니다.
개미굴이 일렬로 되어있으면 최대 깊이가 10000까지 커질 수 있습니다.
- 방이
10^5개 이고, 깊이가 1씩 증가하니 총 방문횟수는 등차수열의 합공식에 의해 다음과 같습니다.1 + 2 + ... + 10^5 = (10^5) * (10^5 + 1) / 2∴ O(N) = 10^10
- 방이
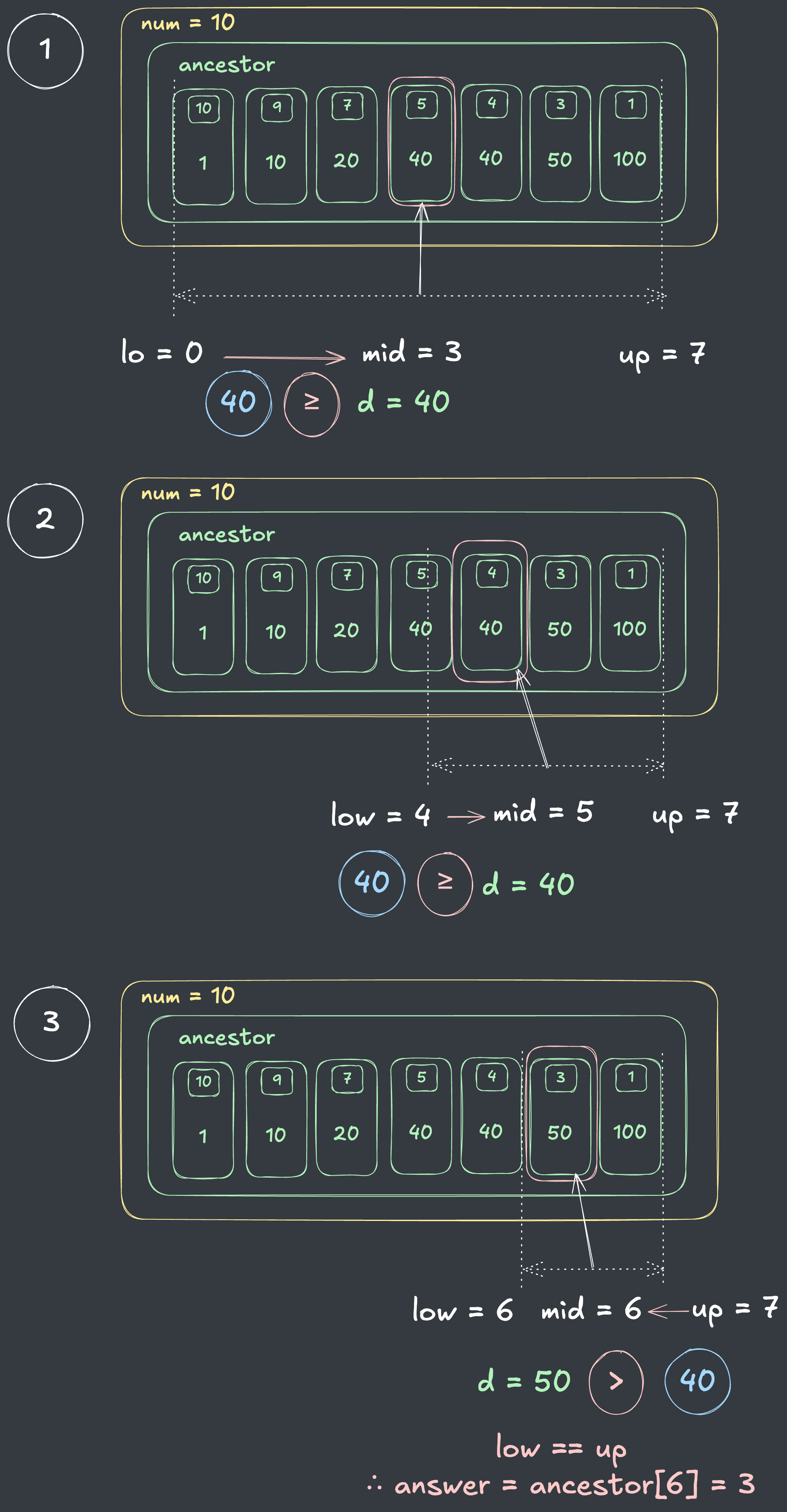
예를 들어, 다음과 같이 부모가
[[10, 1], [9, 10]], [7, 20], [5, 40], [4, 40], [3, 50], [1, 100]이고 개미의 에너지가40인 경우, BinarySearch의 UpperBound를 활용하면 3번만에 최대 도달 가능한 조상의 위치인3를 찾는 것이 가능합니다.